Множественная корреляция. Индекс множественной корреляции, коэффициент детерминации, их свойства и интерпретация.

         Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции: 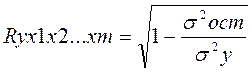 , где s2y  – общая дисперсия результативного признака; s2ост – остаточная дисперсия. Границы изменения индекса множественной корреляции от 0 до 1.   Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции.

 Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии: 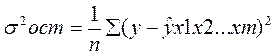 . Можно пользоваться следующей формулой индекса множественной детерминации:

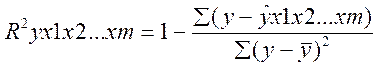
При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением:

где b i – стандартизованные коэффициенты регрессии; r yxi – парные коэффициенты корреляции результата с каждым фактором. Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F -критерия Фишера.