Уравнение множественной регрессии в стандартизированном масштабе. Интерпретация стандартизированных коэффициентов регрессии.

Уравнение множественной регрессии в стандартизированном масштабе:

, где ty, tx1,…,txm – стандартизированные переменные: 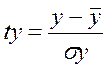, , 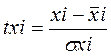для которых среднее значение равно нулю:  , а среднее квадратическое отклонение равно единице: ;  стандартизированные коэффициенты регрессии.

Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор xi изменится на одну единицу при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии bi можно сравнивать между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных  коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Коэффициенты «чистой» регрессии bi связаны со стандартизованными коэффициентами регрессии bi следующим образом: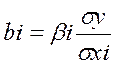. Параметр a определяется как  Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением .Частные коэффициенты эластичности: 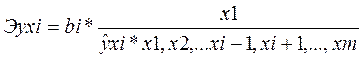 где bi – коэффициент регрессии для фактора x i в уравнении множественной

регрессии,   частное уравнение регрессии.

Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности: 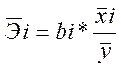которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.