Парная нелинейная регрессия. Критерий для определения параметров модели. Линеаризация моделей.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например y = a + b/ x ; 2. Регрессии, нелинейные по оцениваемым параметрам, например  – y = a × xb – степенная; – показательная – y = a ×bx.

Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных. y =a +b /x может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы и в других случаях. Гипербола приводится к линейному уравнению простой заменой: z =1/ x . Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся, например, степенная функция – y = a × xb, показательная –y = a ×bx . Среди нелинейных моделей наиболее часто используется степенная функция y = a × xb ×e , которой предшествует процедура линеаризации - приводится к линейному виду логарифмированием: ln y = ln(a × xb ×e ); ln y = ln a + b × ln x + lne ; Y = A + b × X + E, где Y = ln y, X = ln x, A = ln a, E = lne . Параметр b – является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Так как для функций коэффициент эластичности зависит от соответствующего значения фактора x , то обычно рассчитывается средний коэффициент эластичности: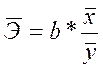  

Построению показательной модели y= a × bx ×e предшествует процедура линеаризации переменных путем логарифмирования ln y = ln( ); ln y = ln a +  x × ln b + lne ; Y = A +  x × B+ E, где Y = ln y, B= ln b, A = ln a, E = lne .

Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости,  дополняется показателем тесноты связи. В данном случае это индекс корреляции:

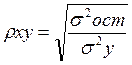, где 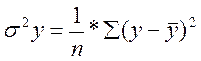– общая дисперсия результативного признака y, 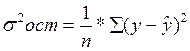– остаточная дисперсия. Величина данного показателя находится в пределах: 0 £ r xy£1. Чем ближе значение индекса  корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака y ,  объясняемую регрессией, в общей дисперсии результативного признака: 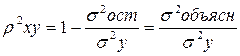т.е. имеет тот же смысл, что и в линейной регрессии; 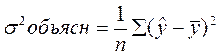Индекс детерминации  r2xy можно сравнивать с коэффициентом детерминации  r2xy для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина  r2xy меньше r2xy. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Индекс детерминации используется для проверки существенности в целом уравнения регрессии по F -критерию Фишера:  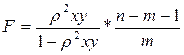 где r2xy  – индекс детерминации, n – число наблюдений, m – число

параметров при переменной x . Фактическое значение F -критерия сравнивается с табличным при уровне значимости a и числе степеней свободы  k 2= n -m -1 (для остаточной суммы квадратов) и  k 1= m (для факторной суммы квадратов). О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по обычной формуле.