После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Проверить значимость уравнения регрессии
– значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации: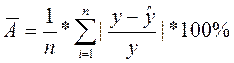 
Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной y от среднего значения y раскладывается на две части – «объясненную» и «необъясненную»: 
где 
– общая сумма квадратов отклонений; 
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов. Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -критерия Фишера: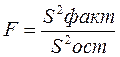 
Фактическое значение F -критерия Фишера сравнивается с
табличным значением F табл( a; k 1; k2 ) при уровне значимости a и степенях свободы k1 = m и k 2= n -m-1.При этом, если фактическое значение F - критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии m =1, поэтому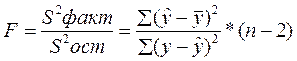 
Величина F -критерия связана с коэффициентом детерминации R2 ее можно рассчитать по следующей формуле: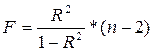 
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: m b и m a. Стандартная ошибка коэффициента регрессии определяется по формул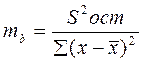е:
, где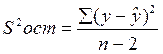 
Величина стандартной ошибки совместно с t –распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала. Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t -критерия Стьюдента: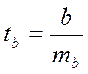 
которое затем сравнивается с табличным значением при определенном уровне значимости a и числе степеней свободы (n-2). Доверительный интервал для коэффициента регрессии определяется как b± tтабл ×mb. Поскольку знак коэффициента регрессии указывает на рост результативного признака y при увеличении признака-фактора x (b>0), уменьшение результативного признака при увеличении признака-фактора (b<0) или его независимость от независимой переменной (b =0), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -1,5 £ b £ 0,8. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра a
определяется по формуле: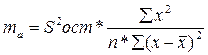 
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется t -критерий: 
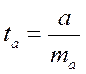, его величина сравнивается с табличным значением при n - 2 степенях свободы.
Поможем написать любую работу на аналогичную тему