Задача 1. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:

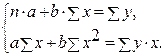
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x2, ∑y2 :

№ п/п	y	х	xy*	x^2	y^2		Ai
1	240	178	42720 Внимание! Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы. Расчет стоимости Гарантии Отзывы	31684	57600	226,189	0,057
2	226	202	45652	40804	51076	225,336	0,003
3	221	197	43537	38809	48841	225,513	0,020
4	226	201	45426	40401	51076	225,371	0,003
5	220	189	41580	35721	48400	225,798	0,026
6	232	166	38512	27556	53824	226,616	0,023
7	215	199	42785	39601	46225	225,442	0,049
8	220	180	39600	32400	48400	226,118	0,028
9	222	181	40182	32761	49284	226,083	0,018
10	231	186	42966	34596	53361	225,905	0,022
11	229	250	57250	62500	52441	223,628	0,024
Итого	2482	2129	480210	416833	560528	2482,0	0,274
Среднее значение	225,64	193,55	43655,45	37893,91	50957,1	225,64

Система нормальных уравнений составит:

Выражая из первого уравнения a и подставляя полученное выражение во второе, получим:

Производя почленное умножение и раскрывая скобки, получим:

Откуда

Тогда

Окончательно уравнение парной линейной регрессии имеет вид:

y= 232,52-0,036 * x

2.2. Рассчитаем параметры уравнений степенной парной регрессии. Построению степенной модели предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

Y=A + bX, где Y = ln y, X = ln x, A = ln a.

После потенцирования получаем: у = еA • хb.

Для расчетов используем данные табл.:

Регион	y	x	Y	X	YX*	Y2	X2
1	240	178	5,48	5,18	28,40	30,04	26,85
2	226	202	5,42	5,31	28,77	29,38	28,18
3	221	197	5,40	5,28	28,52	29,14	27,91
4	226	201	5,42	5,30	28,75	29,38	28,13
5	220	189	5,39	5,24	28,27	29,09	27,48
6	232	166	5,45	5,11	27,84	29,67	26,13
7	215	199	5,37	5,29	28,43	28,84	28,02
8	220	180	5,39	5,19	28,01	29,09	26,97
9	222	181	5,40	5,20	28,09	29,19	27,02
10	231	186	5,44	5,23	28,44	29,62	27,31
11	229	250	5,43	5,52	30,00	29,53	30,49
Итого	2482,00	2129,00	59,60	57,86	313,52	322,97	304,48
Ср.знач	225,64	193,55	5,42	5,26	28,50	29,36	27,68

	(y-yср) 2	(y-)2	(-yср) 2
226,274	206,314	188,391	0,407
225,086	0,132	0,835	0,303
225,321	21,496	18,671	0,099
225,133	0,132	0,753	0,254
225,710	31,769	32,607	0,005
226,933	40,496	25,675	1,681
225,226	113,132	104,576	0,168
226,169	31,769	38,059	0,284
226,117	13,223	16,950	0,231
225,861	28,769	26,413	0,050
223,097	11,314	34,846	6,449
2480,927	498,545	487,777	9,932
225,539	45,322	44,343	0,903

Коэффициенты регрессии
a	b
5,64	-0,042
Потенцирование
a	b
280,76	-0,042

Уравнение степенной парной регрессии имеет вид:

2.3. Рассчитаем параметры уравнений экспоненциальной парной регрессии. Построению экспоненциальной модели предшествует процедура линеаризации переменных.

Для оценки параметров уравнение приводится к линейному виду: ln y = ln a + bx; Y = A + bx, где Y = ln y, A= ln a, .

Затем потенцированием находим искомое уравнение. Искомое уравнение будет: у = eA • ebx

Для расчетов используем данные табл.:

Регион	y	x	Y	x	Yx*	x2
1	240	178	5,48	178,00	975,55	31684,00
2	226	202	5,42	202,00	1094,95	40804,00
3	221	197	5,40	197,00	1063,44	38809,00
4	226	201	5,42	201,00	1089,53	40401,00
5	220	189	5,39	189,00	1019,40	35721,00
6	232	166	5,45	166,00	904,16	27556,00
7	215	199	5,37	199,00	1068,76	39601,00
8	220	180	5,39	180,00	970,85	32400,00
9	222	181	5,40	181,00	977,88	32761,00
10	231	186	5,44	186,00	1012,29	34596,00
11	229	250	5,43	250,00	1358,43	62500,00
Итого	2482,00	2129,00	59,60	2129,00	11535,24	416833,00
Ср.знач	225,64	193,55	5,42	193,55	1048,66	37893,91

	(y-yср) 2	(y-)2	(-yср) 2
226,063	206,314	194,246	0,182
225,251	0,132	0,560	0,148
225,420	21,496	19,538	0,047
225,285	0,132	0,511	0,123
225,691	31,769	32,382	0,003
226,470	40,496	30,586	0,694
225,353	113,132	107,176	0,081
225,995	31,769	35,941	0,129
225,961	13,223	15,691	0,106
225,792	28,769	27,124	0,024
223,637	11,314	28,760	3,997
2480,917	498,545	492,514	5,533
225,538	45,322	44,774	0,503

Коэффициенты регрессии
a	b
5,45	-0,00015
Потенцирование
a	b
232,17	-0,00015

Уравнение экспоненциальной парной регрессии имеет вид:

y = e5,447 *e-0,00015x

2.4. Рассчитаем параметры уравнений полулогарифмической парной регрессии. Построению полулогарифмической модели предшествует процедура линеаризации переменных.

Для оценки параметров она приводится к линейному виду путем замены Х, Х = ln x. Тогда y = a + bX, где

Для расчетов используем данные табл.:

Регион	y	x	y	X	YX*	X2
1	240	178	240,00	5,18	1243,63	26,85
2	226	202	226,00	5,31	1199,67	28,18
3	221	197	221,00	5,28	1167,59	27,91
4	226	201	226,00	5,30	1198,55	28,13
5	220	189	220,00	5,24	1153,18	27,48
6	232	166	232,00	5,11	1185,98	26,13
7	215	199	215,00	5,29	1138,06	28,02
8	220	180	220,00	5,19	1142,45	26,97
9	222	181	222,00	5,20	1154,07	27,02
10	231	186	231,00	5,23	1207,15	27,31
11	229	250	229,00	5,52	1264,41	30,49
Итого	2482,00	2129,00	2482,00	57,86	13054,74	304,48
Ср.знач	225,64	193,55	225,64	5,26	1186,79	27,68

	(y-yср) 2	(y-)2	(-yср) 2
226,402	206,314	184,904	0,586
225,167	0,132	0,694	0,220
225,412	21,496	19,464	0,050
225,216	0,132	0,615	0,177
225,817	31,769	33,833	0,032
227,083	40,496	24,172	2,094
225,313	113,132	106,362	0,104
226,293	31,769	39,601	0,431
226,239	13,223	17,968	0,363
225,973	28,769	25,273	0,113
223,086	11,314	34,980	6,507
2482,000	498,545	487,867	10,679
225,636	45,322	44,352	0,971

Коэффициенты регрессии
a	b
276,99	-9,764
Потенцирование
a	b
276,99	-9,764

Уравнение полулогарифмической парной регрессии имеет вид:

y=276,99-9,764*Lnx

2.5. Рассчитаем параметры уравнений обратной парной регрессии. Для оценки параметров приведем обратную модель 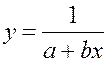к линейному виду, заменив , тогда , где

Для расчетов используем данные табл.:

Регион	y	x	Y	x	Yх*	X^2
1	240	178	0,0042	178,00	0,74	31684,00
2	226	202	0,0044	202,00	0,89	40804,00
3	221	197	0,0045	197,00	0,89	38809,00
4	226	201	0,0044	201,00	0,89	40401,00
5	220	189	0,0045	189,00	0,86	35721,00
6	232	166	0,0043	166,00	0,72	27556,00
7	215	199	0,0047	199,00	0,93	39601,00
8	220	180	0,0045	180,00	0,82	32400,00
9	222	181	0,0045	181,00	0,82	32761,00
10	231	186	0,0043	186,00	0,81	34596,00
11	229	250	0,0044	250,00	1,09	62500,00
Итого	2482,00	2129,00	0,05	2129,00	9,45	416833,00
Ср.знач	225,64	193,55	0,0044	193,55	0,86	37893,91

	(y-yср) 2	(y-)2	(-yср) 2
225,938	206,314	197,747	0,091
225,168	0,132	0,693	0,220
225,328	21,496	18,728	0,095
225,200	0,132	0,641	0,191
225,584	31,769	31,182	0,003
226,325	40,496	32,207	0,474
225,264	113,132	105,340	0,139
225,873	31,769	34,496	0,056
225,841	13,223	14,755	0,042
225,680	28,769	28,298	0,002
223,643	11,314	28,701	3,975
2479,842	498,545	492,787	5,288
225,44	45,32	44,80	0,48

Коэффициенты регрессии
a	b
0,004	0,0000006
Потенцирование
a	b
0,004	0,0000006

Уравнение обратной парной регрессии имеет вид:

2.6. Рассчитаем параметры уравнений равносторонней гиперболы парной регрессии. Для оценки параметров приведем модель равносторонней гиперболы 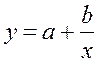к линейному виду.

Гипербола приводится к линейному уравнению простой заменой: z = 1/x . Тогда у = a + b z, где коэффициенты находятся из формул: .

Для расчетов используем данные табл.:

Регион	y	x	y	z	yz*	z2
1	240	178	240,00	0,0056	1,35	0,00003
2	226	202	226,00	0,0050	1,12	0,00002
3	221	197	221,00	0,0051	1,12	0,00003
4	226	201	226,00	0,0050	1,12	0,00002
5	220	189	220,00	0,0053	1,16	0,00003
6	232	166	232,00	0,0060	1,40	0,00004
7	215	199	215,00	0,0050	1,08	0,00003
8	220	180	220,00	0,0056	1,22	0,00003
9	222	181	222,00	0,0055	1,23	0,00003
10	231	186	231,00	0,0054	1,24	0,00003
11	229	250	229,00	0,0040	0,92	0,00002
Итого	2482,00	2129,00	2482,00	0,06	12,96	0,00030
Ср.знач	225,64	193,55	225,64	0,01	1,18	0,00003

	(y-yср) 2	(y-)2	(-yср) 2
226,621	206,314	179,008	0,969
224,971	0,132	1,059	0,443
225,282	21,496	18,332	0,126
225,032	0,132	0,937	0,365
225,813	31,769	33,786	0,031
227,624	40,496	19,148	3,952
225,156	113,132	103,135	0,231
226,466	31,769	41,813	0,689
226,390	13,223	19,276	0,569
226,023	28,769	24,766	0,150
222,622	11,314	40,676	9,085
2482,000	498,545	481,937	16,609
225,636	45,322	43,812	1,510

Коэффициенты регрессии
a	b
212,74	2471,235
Потенцирование
a	b
212,74	2471,235

Уравнение гиперболической парной регрессии имеет вид:

Поможем написать любую работу на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Задача 1. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

Задача 1. Исходные данные

Задача 1. Построить поле корреляции и сформулировать гипотезу о форме связи.

Задача 1. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.

Задача 1. Оценка тесноты связи с помощью показателей корреляции и детерминации

Задача 1. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.

Задача 1. Оценка качества уравнений с помощью средней ошибки аппроксимации.

Задача 1. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.

Задача 1. Рассчитаем прогнозное значение результата по линейному уравнению регрессии

Задача 2. Исходные данные