Задача 1. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.

Рассчитаем коэффициент эластичности для линейной модели:

Для уравнения прямой модели: y= 232,52-0,036 * x

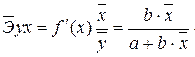
Средний коэффициент эластичности показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 0,031 % от своего среднего значения. Эластичность прожиточного минимума по размеру назначенных ежемесячных пенсий невелика, что вполне согласуется с экономической теорией, а потому небольшое увеличение или уменьшение прожиточного минимума не влечет за собой резкого повышения или понижения размера назначенных ежемесячных пенсий.

Для уравнения степенной модели: :

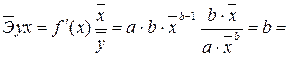-0,042

Он показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 0,042 % от своего среднего значения

Для уравнения экспоненциальной модели: y = e5,447 *e-0,00015x:

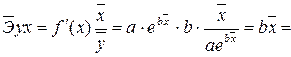
Он показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 0,029 % от своего среднего значения

Для уравнения полулогарифмической модели: y=276,99-9,764*Lnx:

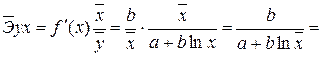
Он показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 0,0374 % от своего среднего значения.

Для уравнения обратной модели: :

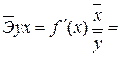
Он показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 0,0275 % от своего среднего значения.

Для уравнения гиперболической модели: :

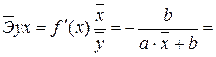
Он показывает, что в среднем при повышении размера прожиточного минимума в месяц на 1% от своего среднего значения сумма среднего размера назначенных ежемесячных пенсий уменьшается на 1 % от своего среднего значения

Сравнивая значения коэффициента эластичности, характеризуем оценку силы связи фактора с результатом:

В данном примере получилось, что самая большая сила связи между фактором и результатом в гиперболической модели, слабая сила связи в обратной модели.