Задача 1. Оценка тесноты связи с помощью показателей корреляции и детерминации

Линейная модель. Тесноту линейной связи оценит коэффициент корреляции. Был получен следующий коэффициент корреляции ,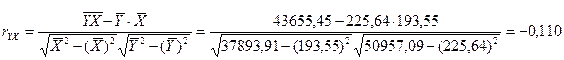

Коэффициент корреляции, равный -0,110, показывает, что выявлена слабая обратная зависимость между размером ежемесячных пенсий и прожиточным минимумом в месяц.

Коэффициент детерминации, равный 0,012, устанавливает, что вариация среднего размера ежемесячных пенсий на 1,2 % из 100% предопределена вариацией размера прожиточного минимума, роль прочих факторов, влияющих на средний размер ежемесячных пенсий, определяется в 98,8 %, что является большой величиной.

Степенная модель. Тесноту нелинейной связи оценит индекс корреляции. Был получен следующий индекс корреляции 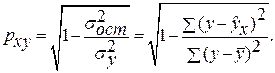=, что говорит о прямой слабой связи. Коэффициент детерминации r²xy=0,022.

Экспоненциальная модель. Был получен следующий индекс корреляции ρxy=0,110, что говорит о том, что связь прямая и слабая. Коэффициент детерминации r²xy=0,012. Это означает, что 1,2% вариации результативного признака (у) объясняется вариацией фактора х.

Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy=0,146, что говорит о том, что связь прямая и слабая. Коэффициент детерминации r²xy=0,021. Это означает, что 2,1% вариации результативного признака (у) объясняется вариацией фактора х.

Гиперболическая модель. Был получен следующий индекс корреляции ρxy=0,183, что говорит о том, что связь прямая слабая. Коэффициент детерминации r²xy=0,0333. Это означает, что 3,3% вариации результативного признака (у) объясняется вариацией фактора х.

Обратная модель. Был получен следующий индекс корреляции ρxy=0,107, что говорит о том, что связь прямая слабая. Коэффициент детерминации r²xy=0,0115. Это означает, что 1,15% вариации результативного признака (у) объясняется вариацией фактора х.

Вывод: по гиперболическому уравнению получена наибольшая оценка тесноты связи: ρxy=0,183 (по сравнению с линейной, степенной, экспоненциальной, полулогарифмической, обратной регрессиями).