Задача 1. Оценка качества уравнений с помощью средней ошибки аппроксимации.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения . Найдем величину средней ошибки аппроксимации :

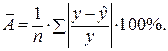
В среднем расчетные значения отклоняются от фактических на:

Линейная регрессия. .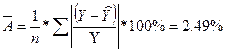

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

Степенная регрессия. .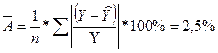

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

Экспоненциальная регрессия. .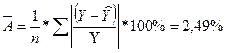

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

Полулогарифмическая регрессия. .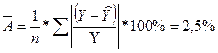

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

Гиперболическая регрессия. .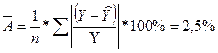

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.

Обратная регрессия. .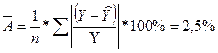

Качество построенной модели оценивается как хорошее, так как  не превышает 8 -10%.