По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.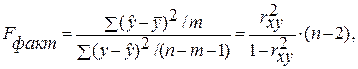 
Линейная регрессия. 
где 
уравнение статистически не значимо
Степенная регрессия. 
где
уравнение статистически не значимо
Экспоненциальная регрессия. 
где
уравнение статистически не значимо
Полулогарифмическая регрессия. 
где
уравнение статистически не значимо
Гиперболическая регрессия. 
где
уравнение статистически не значимо
Обратная регрессия. 
где
уравнение статистически не значимо
Для всех регрессий , из чего следует, что уравнения регрессии статистически не значимы.
|
Вид регрессии |
Уравнение регрессии |
Коэффициент эластичности |
Ошибка аппроксимации |
F-критерий |
|
Линейная |
y=232,52-0,036x |
-0,0305 |
2,49% |
0,110 |
|
Степенная |
|
-0,0416 |
2,5% |
0,199 |
|
Обратная |
|
-0,0275 |
2,49% |
0,0115 |
|
Полулогарифмическая |
y=276,99-9,764*Lnx |
-0,0433 |
2,5% |
0,197 |
|
Гиперболическая |
|
-0,9996 |
2,5% |
0,310 |
|
Экспоненциальная |
y = e5,447 *e-0,00015x |
-0,0290 |
2,5% |
0,11 |
Наибольшее значение коэффициента эластичности и критерия Фишера имеет гиперболическая модель, это значит, что она имеет самую большую силу связи между фактором и результатом и уравнение более статистически значимо чем остальные, значит ее можно взять в качестве лучшей для построения прогноза.
Поможем написать любую работу на аналогичную тему
Реферат
Задача 1. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
От 250 руб
Контрольная работа
Задача 1. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
От 250 руб
Курсовая работа
Задача 1. Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования.
От 700 руб