Множественная и частная корреляция

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

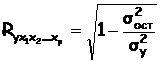, где  - общая дисперсия результативного признака;

 - остаточная дисперсия для уравнения у = f(x1,x2, … ,xp).

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1, чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции. Отсюда ясно, что, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.

Можно воспользоваться следующей формулой индекса множественной корреляции:

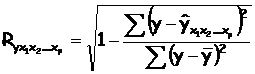
При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

, где - стандартизованные коэффициенты регрессии

- парные коэффициенты корреляции результата с каждым фактором.

Величина множественного коэффициента корреляции зависит не только от корреляции резальтата с каждым из факторов, но и от межфакторной корреляции:

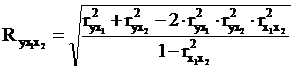
Рассмотренная формула позволяет определить совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов  делится на число степеней свободы остаточной вариации (n-m-1), а общая сумма квадратов отклонения  - на число степеней свободы в целом по совокупности (n-1).

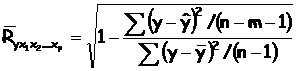
Поскольку =1-R2, то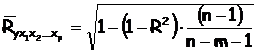

Ранжирование факторов, участвующих в множественной линейной регрессии, может быть проведено с помощью частных коэффициентов корреляции. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.

Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

В общем виде при наличии р факторов для уравнения    y=a+b1x1+b2x2+ … +bpxp+ε

коэффициент частной корреляции, измеряющий влияние на у фактора хi при неизменном уровне других факторов, можно определить по формуле

,

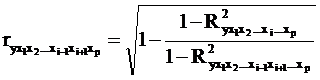 - множественный коэффициент детерминации всего комплекса р факторов с результатом;

 - тот же показатель детерминации, но без введения в модель фактора хр.

При i=1 формула коэффициента частной корреляции примет вид:

.

Данный коэффициент частной корреляции позволяет измерить тесноту связи между у и хi при неизменном уровне всех других факторов, включенных в уравнение регрессии.

Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по формуле

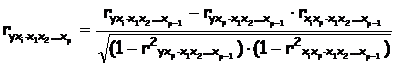
Например, для двух факторов формула примет вид:

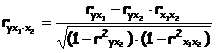 (для i = 1),

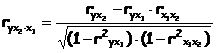(для i = 2).