Анализ коэффициентов уравнения множественной регрессии: 
позволяет сделать вывод о степени влияния каждого из двух факторов на показатель производительности труда. Так, параметр 
свидетельствует о том, что с увеличением продолжительности внутрисменных простоев на 1 мин следует ожидать снижения производительности труда (дневной выработки деталей одним рабочим) на 0,41шт. (обратная связь). Повышение же квалификации рабочего на 1 разряд может привести увеличению выработки на 3,37 детали. Отсюда можно сделать соответствующие практические выводы и осуществить мероприятия, направленные на повышение производительности труда.
Однако на основе коэффициентов регрессии нельзя сказать, какой из факторных признаков оказывает наибольшее влияние на результативный признак, так как коэффициенты регрессии между собой несопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить, в развитии каких факторных признаков заложены наиболее крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариация факторных признаков.
Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности 
, а также бета-коэффициенты 
.
© Различия в единицах измерения факторов устраняют с помощью частных коэффициентов эластичности, которые рассчитывают по формуле:
Частный коэффициент эластичности показывают, на сколько процентов в среднем изменяется признак-результат Y с изменением признака-фактора Х на один процент от своего среднего уровня при фиксированном положении других факторов модели. В случае линейной зависимости Э рассчитываются по формуле:
где ai - коэффициент регрессии при i-м факторе.
© Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью β-коэффициентов, которые вычисляют по формуле:
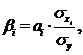
где 
- среднее квадратическое отклонение i-го фактора;
- среднее квадратическое отклонение показателя.
Стандартизированные частные коэффициенты регрессии - β-коэффициенты (b) показывают, на какую часть своего среднего квадратического отклонения
изменится признак-результат Y с изменением соответствующего фактора 
на величину своего среднего квадратического отклонения (sх) при неизменном влиянии прочих факторов (входящих в уравнение).
По коэффициентам эластичности и β-коэффициентам могут быть сделаны противоположные выводы. Причины этого: а) вариация одного фактора очень велика; б) разнонаправленное воздействие факторов на результат.
Кроме того, коэффициент b может интерпретироваться как показатель прямого (непосредственного) влияния фактора (Х) на результат (Y). Во множественной регрессии фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели).
Косвенное влияние измеряется величиной: 
, где т- число факторов в модели. Полное влияние фактора на результат равное сумме прямого и косвенного влияний измеряет коэффициент линейной парной корреляции данного фактора и результата – 
.
Поможем написать любую работу на аналогичную тему