Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности Эi, а также бета-коэффициенты – βi и дельта коэффициенты – Δi.
В общем виде коэффициент эластичности определяется следующим образом:
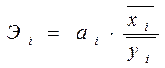(16)
где аi – коэффициент регрессии при i-ом факторе; 
– среднее значение i-го фактора; 
– среднее значение изучаемого показателя.
Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется анализируемый показатель с изменением на 1% каждого фактора при фиксированном положении других факторов.
Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью β-коэффициентов, которые вычисляют по формуле:
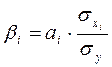(17)
где σxi — среднее квадратическое отклонение i-го фактора; σy - среднее квадратическое отклонение показателя.
β-коэффициент показывает, на какую часть среднего квадратического отклонения изменяется результативный признак с изменением соответствующего факторного признака на величину его среднего квадратического отклонения.
Исходя из соотношения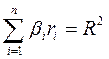 
и принимая во внимание то, что коэффициент множественной детерминации R2 есть доля изучаемых факторов в наличном приращении результативного показателя в анализируемой совокупности, можно сделать вывод, что произведение 
(1≤i≤n) является показателем силы влияния соответствующего фактора на данный показатель.
Поделив произведение ; на коэффициент множественной детерминации R2, получим коэффициент, который показывает какова доля вклада анализируемого фактора в суммарное влияние всех отобранных факторов. Обозначив этот коэффициент Δi, получим
Δi
(18)
На основании частных коэффициентов эластичности Эi βi и Δi - коэффициентов можно судить о резервах роста производительности и эффективности исследуемого процесса, которые заложены в том или ином факторе.
Увеличение числа существенных факторов, включаемых в модель исследуемого показателя, позволяет выявить дополнительные резервы производства.
Для этого могут быть использованы трех-, четырех- (и т.д.), п-факторные регрессии.
Поможем написать любую работу на аналогичную тему