Автокорреляция в остатках. Критерий Дарбина-Уотсона. - Билеты - Эконометрика

Рассматривая последовательность остатков  как временной ряд, можно построить график их зависимости от времени. В соответствии с предпосылками МНК  остатки  должны быть случайными. Однако при моделировании временных рядов нередко встречается ситуация, когда остатки содержат тенденцию или циклические колебания. Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих.  В этом случае говорят об автокорреляции остатков.

Автокорреляция  в  остатках  может  быть  вызвана  несколькими причинами, имеющими различную природу.

1.  Она  может  быть  связана  с  исходными  данными  и  вызвана наличием ошибок измерения в значениях результативного признака.

2.  В  ряде  случаев  автокорреляция  может  быть  следствием неправильной  спецификации  модели.  Модель  может  не  включать  фактор, который  оказывает  существенное  воздействие  на  результат  и  влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными.  Очень  часто  этим  фактором  является  фактор времени t. Либо модель не учитывает несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или фаз циклических колебаний.

От  истинной  автокорреляции  остатков  следует  отличать  ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной  формы  модели.  В  этом  случае  следует  изменить  форму модели,  а  не  использовать  специальные  методы  расчета  параметров уравнения регрессии при наличии автокорреляции в остатках.

Существуют два наиболее распространенных метода определения автокорреляции остатков:

1) построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.

2)  использование критерия Дарбина — Уотсона и расчет величины:

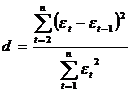
Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Можно показать, что при больших значениях n существует следующее соотношение  между  критерием  Дарбина-Уотсона  d  и  коэффициентом автокорреляции остатков первого порядка :   где

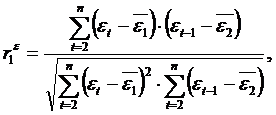
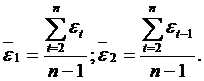
Таким  образом,  если  в  остатках  существует  полная  положительная автокорреляция и  , то  d=0. Если в остатках полная отрицательная автокорреляция, то , следовательно, d=4. Если автокорреляция остатков отсутствует, то    и d=2. Следовательно, 0≤d≤4 .

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина — Уотсона следующий. Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и Н1*  состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках.

Далее по специальным таблицам определяются критические значения критерия Дарбина — Уотсона dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости α. По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой  из  гипотез  с  вероятностью    осуществляется  следующим образом:

 есть положительная автокорреляция. Принимается гипотеза H1 с вероятностью (1- α).

 зона неопределенности.

 автокорреляция остатков нет.

 зона неопределенности.

 есть отрицательная автокорреляция. Принимается гипотеза H1* с вероятностью (1-α).

Если фактическое значение критерия Дарбина — Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу Hо.

Есть несколько существенных ограничений на применение критерия Дарбина — Уотсона:

1.               Он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т.е. к моделям авторегрессии.

2.               Методика  расчета и использования критерия  Дарбина-Уотсона направлена только на выявление автокорреляции остатков первого порядка.

3.               Критерий Дарбина-Уотсона дает достоверные результаты только для больших выборок.