МАССОВЫЕ (ОБЪЁМНЫЕ) И ПОВЕРХНОСТНЫЕ СИЛЫ

Имеется два типа сил, действующих на элемент твёрдой среды: массовые (объёмные)  и поверхностные.

Массовые силы действуют в каждой точке объёма среды.

Величина массовой силы, действующей на элемент среды, пропорциональна его объёму или массе. Например, сила тяжести - вес элемента среды, равный произведению массы на ускорение силы тяжести g. Если ввести плотность среды r, равную массе единицы объёма, то действующую на элемент силу тяжести можно записать как произведение величины  rg  на объём элемента.

Таким образом, сила тяжести, действующая на единицу массы, есть g, а сила тяжести, действующая на единицу объёма  - rg.

Плотность, вообще говоря, зависит от давления. При высоких давлениях, господствующих на больших глубинах в мантии, увеличение плотности пород  может составить до 50% значения плотности при нулевом давлении.

В отличие от массовых сил, поверхностные силы приложены ТОЛЬКО К ПОВЕРХНОСТИ, ограничивающей элемент объёма. Они обусловлены межатомными силами, действующими со стороны материала, находящегося с одной стороны от поверхности, на материал, находящийся с противоположной стороны.

Величина поверхностной силы прямо пропорциональна площади поверхности, на которую она действует. Кроме того, эта сила зависит от ориентации поверхности.

ПРИМЕР: Рассмотрим силу, приложенную к основанию столба породы на глубине у от поверхности Земли и уравновешивающую вес столба. (Рис. 2.1. Массовая и поверхностная силы, действующие на вертикальный столб породы).

Площадь поперечного сечения равна dA;

Вес столба с площадью поперечного сечения dA равен rgydA;

Поверхностная сила, уравновешивающая  этот столб, sууdА направлена вверх и распределена по горизонтальной поверхности площадью dA на глубине у.

ДОПУЩЕНИЯ: на боковые поверхности не действует никаких вертикальных сил и плотность r постоянна.

ТАКИМ ОБРАЗОМ: sуу есть сила, приходящаяся на единицу площади и направленная перпендикулярно горизонтальной поверхности, Т,Е, НАПРЯЖЕНИЕ.

Поскольку силы, действующие на равновесный столб породы, должны быть равны, получаем, что

sуу = rgy.                                          (1)

Сила, приходящаяся на единичную площадь и перпендикулярная горизонтальным плоскостям, линейно растёт с глубиной.

Нормальное напряжение, вызванное весом вышележащих пород, называется ЛИТОСТАТИЧЕСКИМ НАПРЯЖЕНИЕМ или ДАВЛЕНИЕМ.

НАПРИМЕР, литостатическое напряжение в основании континентальной коры при её средней плотности 2750 кг/м3 и толщине коры 35 км  (3.5 ×104 м) будет равно:

sуу = 2750 кг/м3×10 м/с2×3.5×104м = 9.625 ×108Па = 962.5 МПа (9.625 кбар).

В системе СИ единицей давления или напряжения является паскаль (Па);  1 Па = 1 кг×/м×с2;. 1 мегапаскаль МПа = 106 Па; 1 бар = 105 Па = 0.98692 атм.

Поскольку плотность жидкой мантии (3300 кг/м3 ) больше плотности пород континента (2750 кг/м3), то можно считать, что континент является блоком, плавающим в мантии (Рис.2.2. Континентальный блок, "плавающий" на "жидкой" мантии.) Согласно закону Архимеда, выталкивающая сила, действующая на континент,  равна весу вытесненной мантийной породы. В основании континента напряжение sуу = rкgh, где rк - плотность континентальных пород, h - толщина континента. На этой же глубине в мантии напряжение составит sуу = rмgb, где rм - плотность мантии, b - глубина погружения континента в мантию.

С другой стороны, согласно гидростатическому равновесию эти два напряжения должны быть равны:

rкgh = rмgb, т.е. rкh = rмb.                                                (2)

Применительно к континентальной коре принцип гидростатического равновесия называется ПРИНЦИПОМ ИЗОСТАЗИИ.

Откуда можно определить:

1.    Возвышение континента над окружающей мантией:                                              h - b = h - rк/rмh = h (1-rк/rм);                                                  (3)

2.     Глубину океанического бассейна относительно поверхности континента (Рис.2.3. Структура континентального и океанического регионов):

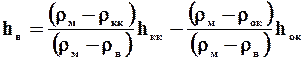                                     (4)

где:

Ø hкк, rкк  - толщина и плотность континентальной коры;

Ø hв  -  глубина океана;

Ø rв - плотность воды;

Ø hок - толщина океанической коры;

Ø rок - плотность океанической коры;

Ø rм - плотность мантии.