ИНТЕНСИВНОСТЬ ДЕФОРМАЦИЙ СДВИГА

Величины g1 = e2 - e3 ,  g2 = e3 - e1 , g3 = e1 - e2 - называются ГЛАВНЫМИ СДВИГАМИ

G » 1.08 gmax

где gmax   - наибольший из главных сдвигов.

В произвольной декартовой системе координат величина Г вычисляется по формуле

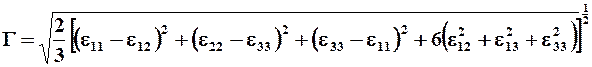.(1.22)

Иногда используется величина, которая называется интенсивностью деформации, или приведённой деформацией

.

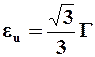Для характеристики деформационного состояния служит параметр Надаи

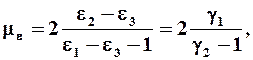                                                         (1.23)

который изменяется от - 1 (при чистом удлинении) до + 1(при чистом укорочении). В случае чистого сдвига он равен 0. При всестороннем расширении или сжатии параметр me не имеет смысла.

Часто компоненты деформации представляют в следующем виде:

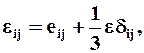                                                                                      (1.24)

где   eij - компоненты, характеризующие только деформации сдвига, называются компонентами девиатора деформаций;  dij - символ Кронекера.

Отсюда следует,  что компоненты тензора деформации растяжения (сжатия) eii отличаются от соответствующих компонент девиатора eii на 1/3 объёмной деформации, а компоненты деформации сдвига не отличаются, т.е.

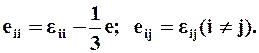
Если известны компоненты деформации eij как функции декартовых координат xi, то для однозначного определения трёх компонент ui  вектора перемещений из шести соотношений (1.20) НЕОБХОДИМО И ДОСТАТОЧНО, чтобы функции  eij  удовлетворяли условиям совместимости (ИЛИ НЕРАЗРЫВНОСТИ) деформаций Сен-Венана:

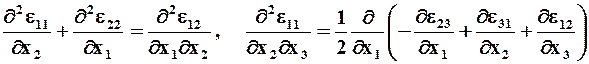(1.25)

и т.д., всего шесть условий (остальные получаются из выписанных круговой заменой индексов 1 ® 2 ® 3 ® 1).

Таким образом, условия совместимости (1.25) являются уравнениями, связывающими компоненты  eij тензора деформаций.

Для анализа больших деформаций, если главные оси при деформации не поворачиваются, используются НАТУРАЛЬНЫЕ УДЛИНЕНИЯ (укорочения)

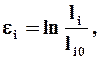
где li0, li  - начальные и текущие длины элемента в соответствующих направлениях.

Характерные соотношения для малых деформаций являются справедливыми и для натуральных удлинений.

Если скорость частиц сплошной среды `v = (v1, v2, v3),  то за бесконечно малый промежуток времени dt среда испытывает бесконечно малую деформацию, определяемую перемещениями  ui = vidt (i =1, 2, 3).

Компоненты этих деформаций, вычисленные по формулам (1.20), имеют общий множитель dt, разделив на который получаем

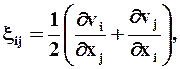                                                              (1.26)

где  xij - компоненты тензора скоростей деформаций.

Величины  xij  определяют скорости удлинения (укорочения) единичных отрезков в направлениях  Oxi, xij (i ¹ j)    - угловые скорости изменения первоначально прямых углов, составленных единичными отрезками вдоль координатных осей.

Подобно формуле (1.19) скорость удлинения (укорочения) любого единичного отрезка вычисляется по формуле

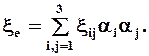
Аналогично соотношениям (1.21) - (1.23) инвариантами скорости деформации являются:

ü скорость относительного объёмного расширения (сжатия)

x = x11 + x22 + x33 = x1 + x2 + x3 = div`v;                                            (1.28)

ü интенсивность скоростей деформации сдвига относительно главных осей

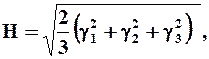                                                      (1.29)

где  g1 = x2 - x3,  g2 =  x3  - x1,  g3 = x1 + x2  - главные скорости сдвигов (относительно произвольной системы координат Н выражается формулой 1.22);

ü параметр Надаи  wx  = 2g1 / g2  - 1.

Компоненты скоростей деформации xij , как и компоненты деформации eij не могут быть произвольными. Они должны удовлетворять условиям совместимости (аналогичным условиям 1.25).

Подобно (1.24) для компонент тензора {xij} скоростей деформаций верно соотношение

xij = lij + 1/3xdij,                                                           (1.30)

где  lij - компоненты, характеризующие только скорости деформации сдвига, называемые компонентами девиатора скорости деформаций.