БАЗОВЫЕ ЗАДАЧИ ГИДРОДИНАМИКИ ПРИ ПРОМЫВКЕ И ЦЕМЕНТИРОВАНИИ СКВАЖИН

При промывке и цементировании скважин простейшими базовыми задачами гидромеханики, допускающими аналитическое решение, являются задачи о течении жидкости в плоской щели (между двумя параллельными бесконечными пластинами) в круглой трубе и в кольцевом пространстве между двумя соосными цилиндрами.

Для их решения необходимо исходить из следующих условий:

Ø жидкость несжимаема (r = const);

Ø течение установившееся ();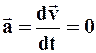

Ø все частицы жидкости движутся параллельно твёрдым стенкам канала, что означает, что при совмещении координатной оси Oz с направлением течения, отличной от нуля будет лишь одна составляющая vz скорости

Ø концевые эффекты пренебрежимо малы, то есть, картина течения в любом сечении, нормальном к потоку, идентична 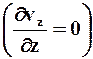, что справедливо для сечений, удалённых от концов канала на расстояние равное 0.035 d ×Re, где d - характерный размер поперечного сечения: для щели - это расстояние между плоскостями; для трубы - её диаметр; для кольцевого пространства - удвоенный зазор;

Ø вдоль потока действует постоянный градиент давления    равный , где Dр > 0 - полный перепад давления между двумя сечениями, находящимися  на расстоянии  L друг от друга;

Ø на жидкость действует объёмная сила  Fz = ±rg (Fx = Fy = 0), обусловленная только силой тяжести, где принимают знак (+) если жидкость движется вниз, и знак (-) - вверх, когда положительное направление оси Оz  совпадает с направлением движения.

Скорости частиц жидкости в рассматриваемых каналах симметричны относительно плоскости yz  - для щели и относительно оси Oz - для круглой трубы и кольцевого пространства, то vz = v(x)  и vz= v(r) соответственно.

Поэтому, согласно соотношениям Коши (2.15). уравнениям состояния (2.14) при течении жидкости в щели, отличными от 0 будут только одна СКОРОСТЬ ДЕФОРМАЦИИ и одно НАПРЯЖЕНИЕ СДВИГА:

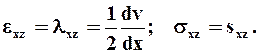(2.18)

Для течения в трубе и кольцевом пространстве

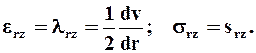 (2.19)

Система дифференциальных уравнений (2.11)- (2.14) существенно упрощается:

Ø уравнения движения и уравнения неразрывности удовлетворяются тождественно;

Ø уравнение механического состояния в плоской щели принимает вид:

 ,

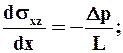а в кольцевом пространстве

,

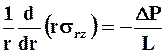где:  DR = Dp ± rgL - гидродинамические потери давления, обусловленные только движением жидкости независимо от направления течения.

Интегрирование этих уравнений при условиях sxz = 0 при х = 0 для щели и srz = 0 при  r = 0 для круглой трубы приводит к выражениям:

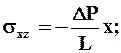(2.20)

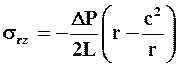(2.21)

где постоянная интегрирования с2 ¹ 0 только при течении жидкости в кольцевом пространстве.

ЗАПОМНИТЕ, что соотношения (2.18)-(2.21) справедливы при ламинарном течении ЛЮБОЙ жидкости (ньютоновской или неньютоновской). Сохранятся они и при турбулентном режиме течения, но под величинами v, DP,sxz, srz , будут пониматься усреднённые по времени значения этих величин:

.

Далее рассматриваются аналитические решения граничных задач течения жидкости в щели и в кольцевом пространстве (в зависимости от характера течения и реологических свойств жидкости).

При этом определяются основные интегральные гидродинамические характеристики потока: объёмный расход Q, средняя скорость vср , коэффициент сопротивления  l.

Определение объёмного расхода  по заданному перепаду давления обычно называют ПРЯМОЙ ЗАДАЧЕЙ ГИДРОДИНАМИКИ, а определение перепада давления по заданному расходу - ОБРАТНОЙ.

Все результаты, рассматриваемые далее, относятся к решениям прямой граничной задачи, а полученные зависимости используются для ВЫЧИСЛЕНИЯ ГИДРАВЛИЧЕСКИХ ПОТЕРЬ. Для этой цели определяется закон сопротивления, т.е. зависимость коэффициента l от характеристик течения.

Основополагающей задачей гидродинамики (гидравлики) является экспериментальное установление закона сопротивления.

Если l не зависит от DР, то для коэффициента сопротивления получаем известный закон Дарси -Вейсбаха, широко используемый для определения гидравлических потерь в цилиндрических каналах при турбулентном режиме течения:

.

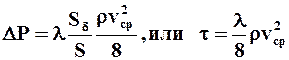Ламинарное и турбулентное течение жидкостей в щелевом канале

1.     Ламинарное течение неньютоновской жидкости.

Согласно соотношениям (2.18), отличными от 0 будут лишь одна скорость деформации и одно напряжение сдвига и сохранится только одно уравнение состояния

,

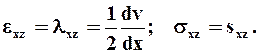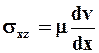(2.23)

Сравнивая это уравнение с решением (2.20)

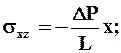
получим дифференциальное уравнение относительно скорости

,

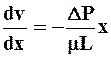решение которого, при граничном условии v(h) = 0, (2h - ширина щели) имеет вид

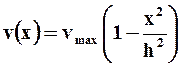. (2.24)

Используя формулы (2.22) можно определить основные характеристики потока:

Ø объёмный расход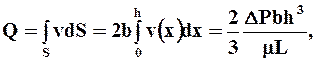

Ø среднюю скорость

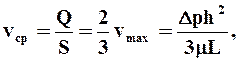
Ø коэффициент сопротивления

,

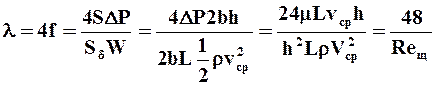где S, Sd - соответственно площади поперечного сечения и боковой смоченной поверхности канала; f = t / W- коэффициент трения Фаннинга; 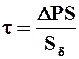 - касательное напряжение у поверхности канала; 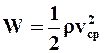- кинетическая энергия единицы объёма жидкости; b - длина поперечного сечения щели;  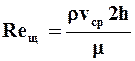     - параметр Рейнольдса для плоской щели.

Например:

при r = 1000кг/м3;   vср = 1 м/с;  2h  = 0.01 м; m  = 0.01 Па ×с

ИМЕЕМ:  Reщ  = 1000; l  = 0.048;  DP/L = 1200 Па/.

ВЫВОД:   на каждые 1000м  гидравлические потери составят 1.2 МПа.

2.     Ламинарное течение жидкости Шведова - Бингама.

Пользуясь тем же уравнением (2.18), и подставляя его в (2.16- интенсивность касательных напряжений) и (2.17- интенсивность скорости деформации сдвига при скорости деформации объёма x = 0) будем иметь:

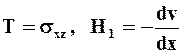 (2.26).

Знак (-) выбран из-за того, что .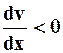

Система уравнений упрощается до одного уравнения (2h0 - жёсткое ядро потока, см. рис.7, стр.43.  Характерный вид профиля скорости в щели при течении неньютоновской жидкости Шведова-Бингама):

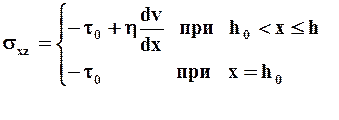(2.27)

Сравнивая уравнение (2.27) с (2.20) получим уравнение скорости

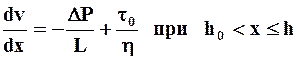 (2.28)

и формулу для вычисления ядра потока

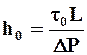  (2.29)

Интегрируя уравнение (2.28) при v (h) = 0, найдём следующее распределение скорости:

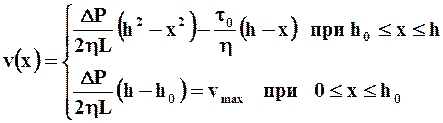(2.30)

Отсюда следует:

Ø при  h0 = h  движение жидкости происходить не будет, т.к. v (x)  = 0;

Ø условием существования движения является h0 < h или, используя формулу (2.29),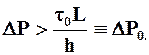

Однако, если учесть, что начало движения рассматриваемой жидкости обусловлено не динамическим напряжением сдвига t0, а статическим t00 > t0, то условием страгивания покоящейся жидкости будет .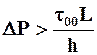

По формулам (2.22) определяют основные характеристики потока (впервые получены М.П. Воларовичем и А.М. Гуткиным):

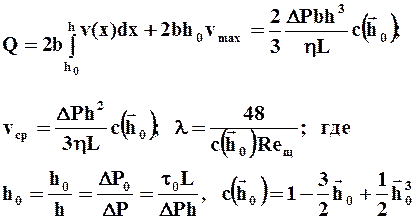   (2.31)

Как видно из полученных выражений, кинематические характеристики потока Q, vср и коэффициент сопротивления l зависят от градиента давления нелинейно, что вызывает трудности при решении обратной задачи.

Если исходить из того, что практический интерес представляют случаи, когда  DР >>DR0 (`h0<<1), то, приняв  c (`h0) = 1 - 3/2`h0, получим

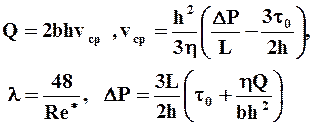(2.32)

где 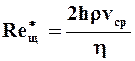  - обобщённый параметр Рейнольдса;  h* = h (1+ 1/4Senщ)  - приведённая вязкость жидкости Шведова - Бингама;  Senщ = t02h/hvср - параметр Сен - Венана для плоской щели.

Например, при r  = 1350 кг/м3,  t0 = 5 Па, h  = 0.04 Па ×с;  vср = 1 м/с,  h = 0.02 м.

ПОЛУЧИМ:

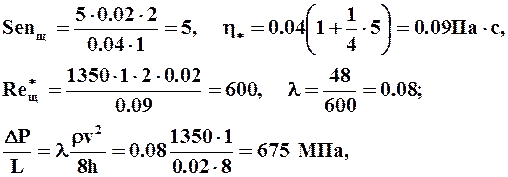
т.е. в этом случае на каждые 1000 м гидравлические потери составляют 0.675 МПа.

3.    

Неньютоновская жидкость Освальда - Вейля.

Используя в системе (2.14) соотношения (2.18) и (2.26), получим:

Сопоставляя это уравнение состояния с решением (2.20) приходим к дифференциальному уравнению относительно скорости:

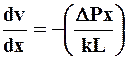 (2.33)

Интегрируя это уравнение при граничном условии v (h) = 0, получим распределение скорости:

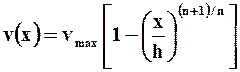 (2.34)

где:                                .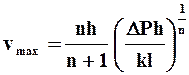

Интегральные характеристики потока при этом будут:

;

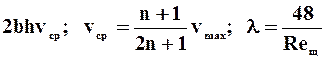где 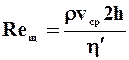   - обобщённый параметр Рейнольдса и  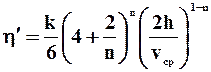- приведённая вязкость жидкости Освальда -Вейля для плоской щели. При  n = 1 и  k =  m формулы (2.34) -  (2.35) совпадут с формулами (2.24) - (2.25).

4.     Турбулентный режим течения. Когда параметры   ,   или   больше критических значений, решение уравнения движения записывается в виде (сравните с 2.20):

.

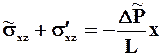Касательное напряжение   в зависимости от типа жидкости связано со скоростью сдвига    уравнениями вида (2.23), (2.27) или (2.33). Напряжение Рейнольдса    в силу соотношений (2.10), (2.18) и (2.26)  удовлетворяет уравнению Прандтля:

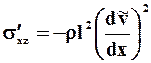, (2.37)

где принимается, что величина l линейно зависит от расстояния до стенки канала   s = h  - х , т.е.

l = æs (2.38)

где  æ - константа, определяемая из опыта.

Напряжение    имеет существенное значение лишь в непосредственной близости от стенок канала, т.е. в узкой области, состоящей из ламинарного подслоя и буферной зоны, где ламинарные и турбулентные законы течения сравнимы между собой.

В основной области течения (турбулентное ядро) можно пренебречь напряжением. Поэтому после подстановки (2.37) и (2.38) в (2.36) получим следующее исходное дифференциальное уравнение: