Дифференциальное уравнение неразрывности потока.

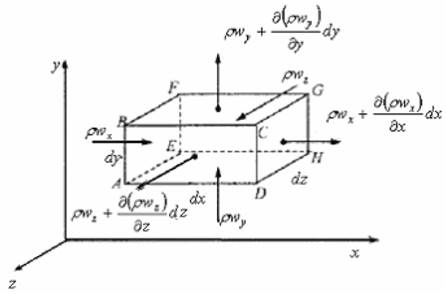
Выделим в движущемся потоке элементарный объем в форме прямоугольного параллелепипеда (рис.) и определим изменение массы  жидкости в выделенном объеме за элементарный промежуток времени . Это изменение массы определяется разностью между втекающей и вытекающей массой жидкости через грани элементарного объема. Поскольку объем выделенного элемента  остается неизменным с течением времени, то изменение массы жидкости  может быть обусловлено лишь изменением ее плотности.  

Определим массу жидкости, втекающую в выделенный объем за единицу времени. Жидкость втекает через грани  в следующих количествах: через грань ; через грань ; через грань .

 Жидкость вытекает через грани  в следующих количествах: через грань через грань через грань

Просуммировав количества втекающей и вытекающей жидкости по всем граням, найдем изменение массы жидкости в выделенном объеме:

Это уравнение называется дифференциальным уравнением неразрывности или сплошности. Оно также может быть записано в виде

 Для потоков несжимаемой жидкости (стационарных и нестационарных)

уравнение неразрывности примет вид Для стационарных потоков газа (сжимаемой жидкости) уравнение неразрывности примет вид Необходимо отметить, что существуют и другие способы вывода уравнения неразрывности.