Дифференциальные уравнения движения идеальной жидкости Л. Эйлера и реальной  жидкости Навье – Стокса

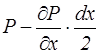  1 -;  2 -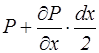

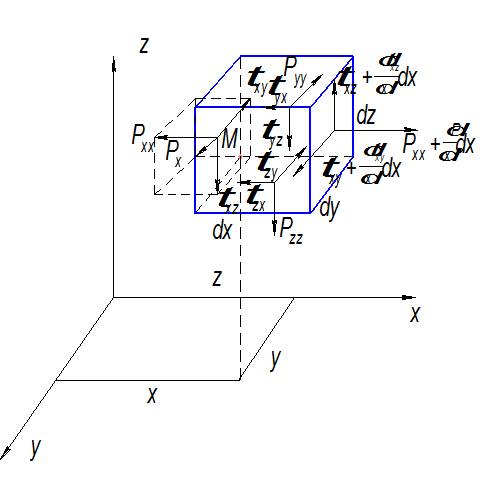
Рассмотрим бесконечно малый объем Ж в форме элементарного параллелепипеда с ребрами dx, dy, dz , движущуюся относительно неподвижной системы координат xyz.

Воспользуемся теоремой о движении центра масс частиц: произведение массы частиц на ускорение их центра масс равно сумме всех внешних сил, действующих на частицы.

;;

Поверхн-ые силы: на левую грань парал-да:;на правую: .

Силы трения Т=0, так как Ж идеальная( невязкая).

Массовые силы:

;;            

 X,Y,Z – проекции ускорений массовых сил на оси координат.

Составим выражение  на ось х.

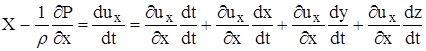
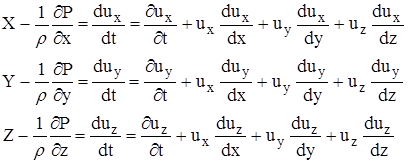     1755г - ДУ движ-ия ид. Ж Эйлера.

Неизвестные . Известные X, Y, Z, ρ.

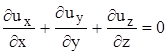.                Есть только частные решения, общих нет.

При движении реальной Ж возникают касательные напряжения, которые дают трение( силу трения)

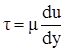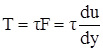, , F – площадь трения.

Уравнения Эйлера для идеальной Ж имеют вид:

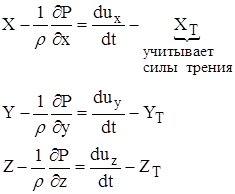
“+” – если растягивает.

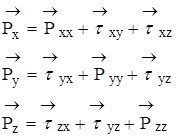
Для идеальной Ж

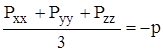
Составим сумму проекций сил на ось х:

На левую грань: 

На правую грань:

Результирующее усилие от нормального напряжения

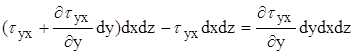
Сумма сил, действующих по оси х, у и z:

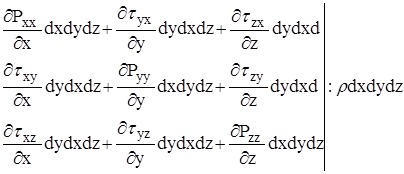
Рхх  - нормальное напряжение; первый индекс – грань, перпендикулярная оси х( yz); второй – проекция этого напряжения на координатную ось.

Аналогично Руу, Рzz, , …

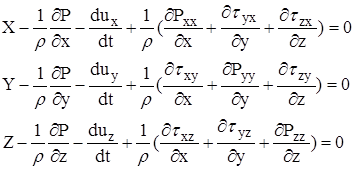 - ДУ движения реальной Ж в напряжениях.

Воспользуемся законом Ньютона о касательных напряжениях:

;                ;

;                 ;

;                 .

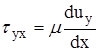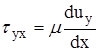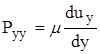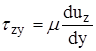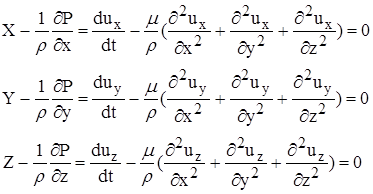-ду движения реальной Ж  Н-Стокса( 1846г.)