Рассмотрим равномерное ламинарное течение в круглой трубе
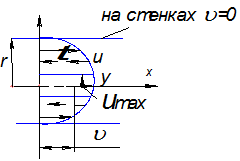
![]() ;
;![]()
Возьмем цилиндрический объем движения жидкости
радиусом ![]() и применим к нему основное уравнение
и применим к нему основное уравнение
равномерного движения:
![]() (*);
(*);![]() ;
;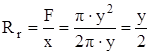 -гидравлический радиус
-гидравлический радиус
![]() - гидравлический уклон:
- гидравлический уклон:
Используем закон Ньютона-Петрова: 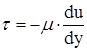 (**); “–“ т.к вдоль оси y υ↓
(**); “–“ т.к вдоль оси y υ↓
Приравниваем (*) и (**):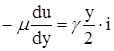 ;
;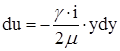 - интегрируем:
- интегрируем: 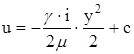
На стенке: при![]() ;
; ![]() , тогда получаем
, тогда получаем 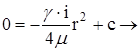
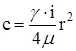
Закон распределения скоростей: 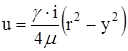 -уравнение параболы
-уравнение параболы
При ![]() на оси
на оси ![]()
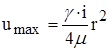 ;
; 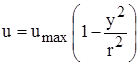
Найдем среднюю скорость при ламинарном режиме:
Рассмотрим полусимметричный слой жидкости радиусом y и толщиной dy:
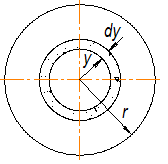
Найдем расход жидкости через этот слой
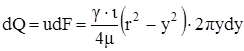 -элементарный расход жидкости через слой;
-элементарный расход жидкости через слой; ![]() . Расход через все сечение:
. Расход через все сечение:
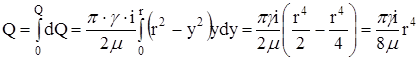
Средняя скорость: 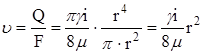
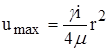 ;
; 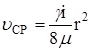 , получим:
, получим: ![]()
Средняя скорость равна половине максимальной скорости. Коэффициент Кориолиса:
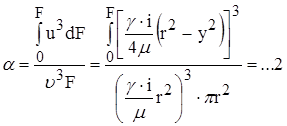
Получим формулу для определения потери напора по длине трубы:
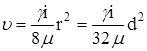 ,
,
Гидравлический уклон: 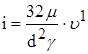 ,
,![]()
Формула Пуазейля: 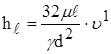 (1)
(1)
Потери напора по длине зависят от рода жидкости (![]() ), длины трубы (
), длины трубы (![]() ), от сечения трубы (
), от сечения трубы (![]() ) и не зависят от состояния поверхности ; i зависит от вязкости.
) и не зависят от состояния поверхности ; i зависит от вязкости.
(1) умножим и разделим на (2![]() )
)
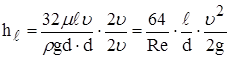 ;
;
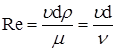 ;
;
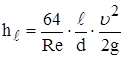
Обозначим ![]() -коэффициент сопротивления трения
-коэффициент сопротивления трения
Формула Дарси-Вейсбаха: 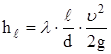
Параболический закон распределения скоростей по сечению трубы наступает не сразу при входе жидкости в трубу, а лишь на некотором начальном участке.
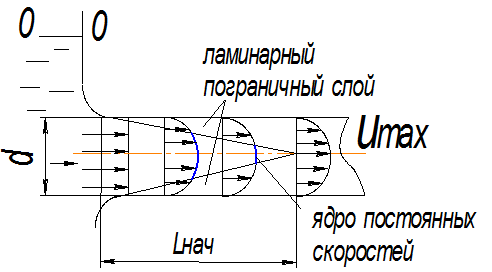
![]() (
(![]() )
)
За длину начального участка принимается условно такое расстояние от входа до сечения, где скорость распределения по параболическому закону с точностью в 1%
![]()
Потери напора при движении по сечению 0-0 и х-х: 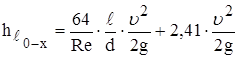
Поможем написать любую работу на аналогичную тему
Реферат
Ламинарное течение жидкости в трубах. Распределение скоростей и потери напора по длине трубы.
От 250 руб
Контрольная работа
Ламинарное течение жидкости в трубах. Распределение скоростей и потери напора по длине трубы.
От 250 руб
Курсовая работа
Ламинарное течение жидкости в трубах. Распределение скоростей и потери напора по длине трубы.
От 700 руб

