Можно предполагать, что обобщенная гипотеза Ньютона, а значит и опирающееся на неё уравнение Навье–Стокса справедливы как при ламинарном, так и при турбулентном режиме движения жидкости; однако использовать данное уравнение Навье–Стокса для турбулентного режима движения практически невозможно. Входящие в них мгновенные скорости и давления являются пульсирующими величинами, поэтому для турбулентного режима ставится задача отыскания осредненных во времени скоростей и давлений. Для получения уравнений Рейнольдса используется уравнение Навье-Стокса, все члены которых подвергаются операции осреднения во времени.
Операции осреднения основаны на предположении о существовании для любого турбулентного движения такого интервала осреднения Т, что выполненные по нему осреднения дают величину неизменяющуюся при повторном осреднении. Операция осреднения проводится по определенным правилам. Пусть:
и
-зависимые переменные, которые необходимо осреднить и пусть 
-пусть одна из четырех зависимых переменных: х, у, z, t
Правило осреднения обладает четырьмя свойствами
1) 
; 2)
; 3)
; 4)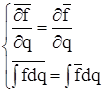
Пульсационные составляющие скоростей охарактеризованы частотой и амплитудой. Средние амплитуды пульсации скоростей характеризуются величинами:
;
;
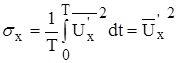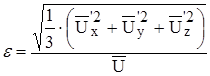-степень турбулентности потока
-продольная составляющая 
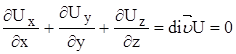-несжимаемая жидкость
-осредненное значение
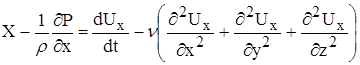-уравнение Н-Стокса для несжимаемой Ж
Оператор Лапласа 
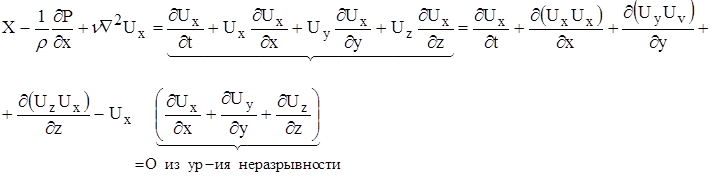
Осредняем:
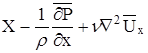
При установившемся движении: 
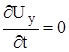
Уравнение Рейнольдса для турбулентного режима:
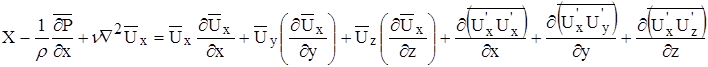
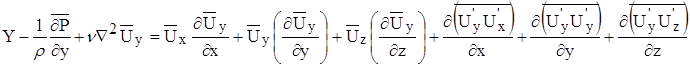
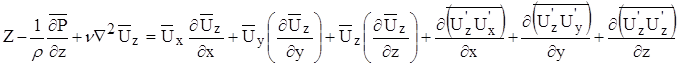
Система уравнения незамкнутая
-отражает чисто вязкостное трение (
в)
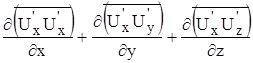-за счет турбулентного перемешивания
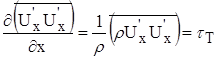-касательное напряжение за счет турбулентного перемешивания
(Па)
Поможем написать любую работу на аналогичную тему