Подобие гидротехнических процессов: геометрическое, кинематическое и динамическое. Числа и критерии подобия

 Физически подобные явления – явления одной и той же физической природы, для которой все характерные величины подобны: в сходственных точках пространства и в соответственные моменты времени для подобных явлений все векторные величины д/б геометрически подобными, а скалярные – соответственно пропорциональными.

Сходственными точками механически подобных систем наз-ся точки одинаково расположенные по отношению к границам этих систем.

При физическом моделировании на сходственные точки натуры и модели должны действовать силы одной и той же механической природы – одноименные силы (сила тяжести, трения, давления).

При моделировании гидравлических явлений различают подобия: динамическое, кинематическое и геометрическое.

1) геометрическое подобие: две гидравлические системы будут геометрически подобными в том случае, если м/д сходственными размерами этих систем всюду существует постоянное соотношение: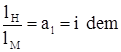; lН – линейный размер натуры; lМ - линейный размер модели; аl – линейный масштаб.

М/д площадями: 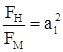 ; М/д объемами: 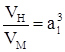; Углы:.

2) кинематическое подобие: два потока будут кинематически подобными при подобии полей скоростей и ускорений натуры и модели.

;

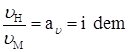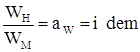
Время протекания соответствующего явления: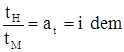

Кинематическое подобие

имеет место только при

наличии геометрического

подобия.

3) динамическое подобие: 2 гидравлические системы будут динамически подобными, если многоугольники сил, построенные для любых 2-х сходственных точек рассматриваемых систем явл-ся геометрически подобными, причем масштаб сил оказывается одинаковым для всех пар сходственных точек.

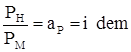
Для кинематически подобных систем: ;

Критерии динамического подобия:

В общем виде  на движущуюся Ж действуют силы:

1) сила тяжести G 2); сила трения (внешняя, внутренняя) Т; 3) давления Р; 4) сила инерции J.

1. Действие силы тяжести и инерции

; .

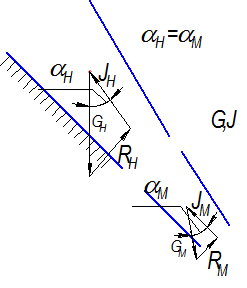
Отношение ускорений: 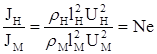 - число

Ньютона; ;

.

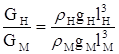Из подобия треугольников сил:

, тогда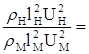

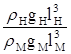
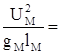
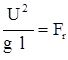;  - число Фруда.

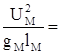
; ; Fr – отношение силы инерции к силе тяжести:

2. Действие силы трения Т

; ; ;

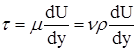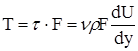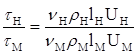Масштаб всех сил одинаков, тогда ; ; =

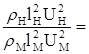
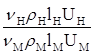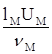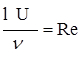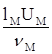; =; ; Re =.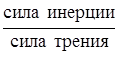

2. Действие силы давления Р

Р=рF;

Отношение силы инерции: 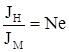 - масштаб силы = ар (критерий Ньютона)

Из подобия треугольников сил: , тогда ; .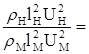

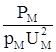
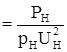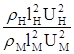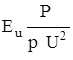;  - число Эйлера.

; ;

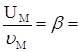
Критерий подобия можем выразить ч/з местные скорости:

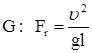
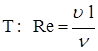
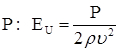
М= - число Маха

Пусть одновременно действуют два критерия: Фрудо и Re:

==

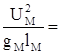
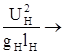
gH=gM:    ==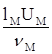

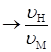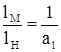
νH=νM – кинематический коэффициент вязкости

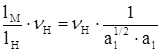 ; аl = 30  

Заключаем: полного подобия нельзя достигнуть, т.к разные критерии подобия требуют различных соотношений разных параметров (скоростей, расходов), поэтому моделирование осуществляют по главному критерию подобия, отвечающему главной действующей силе.

Для безнапорных потоков: Fr – критерий; для напорных – Rе.