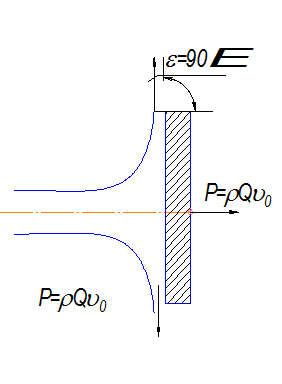
Воздействие струи на преграду. Удар симметричный:
Сила давления струи на неподвижную преграду
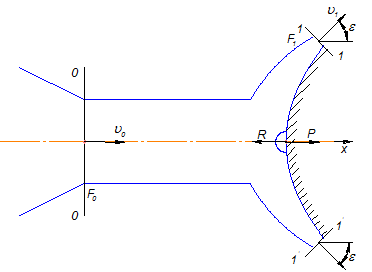 Струя после удара делится на 2
Струя после удара делится на 2
равные части.
Применим к части Ж м/д
сечениями 0-0; 1-1 и 1’-1’ теорему
об изменении кол-ва движения в
проекции на ось х:
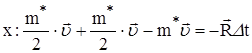 ;
;
![]()
m*-простая масса;
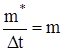 -массовый расход
-массовый расход
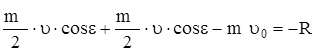 ;
; ![]()
Ур-ие постоянства расхода для сечений 0-0; 1-1; 1’-1’ : ![]() ;
;
F0=2F1 – из условия сплошности;
 !
! ![]() ; m- массовый расход
; m- массовый расход
Плоская преграда: Преграда в виде ковша:
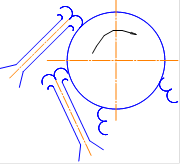 Подвижная преграда:
Подвижная преграда:
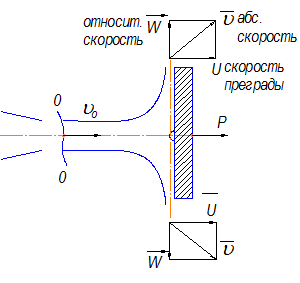 Подвижная плоская преграда:
Подвижная плоская преграда:
![]()
![]() -сила давления на
-сила давления на
подвижную преграду.
Мощность, которую несет за собой подвижная
преграда: ![]()
U-переносная скорость; ![]()
При U=0 – неподвижная преграда
![]() ;
;![]()
При U=υ0 Р=0, ![]()
При Q=const υ0= const
![]()
Найдем максимальное значение этой ф-ии: ![]() ;
;
ρ≠0; Q≠0, тогда ![]() ;
; ![]() ;
;
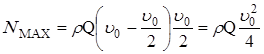 -теоретически; в действительности:
-теоретически; в действительности: ![]()
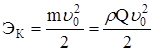 -мощность;
-мощность; ![]()
Остальная часть энергии: струя на выходе из преграды имеет ![]() : при
: при 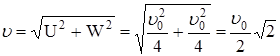 ,
, 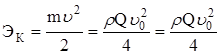
Неиспользованная мощность струи заключена в потоке сходящей с преграды с абс. ![]()
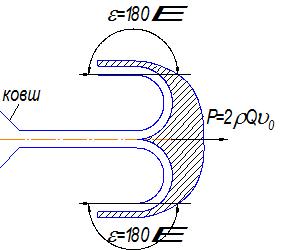
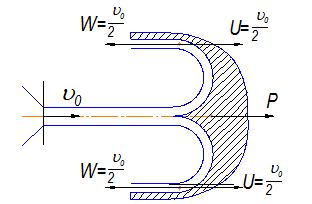 Для использования этой энергии используют преграду в виде ковша с разворотом на 1800:
Для использования этой энергии используют преграду в виде ковша с разворотом на 1800:
![]() ;
; ![]()
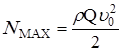
Поможем написать любую работу на аналогичную тему

