Основные положения теории вероятностей, важные для решения задач теории надежности строительных конструкций

Событие - качественный или количественный результат опыта, осуществляемого при определенных условиях. Например, событие - попадание предела текучести стали  в интервал от 240 до 260 МПа. Событие может быть случайным, достоверным или невозможным. Объективная математическая оценка возможности реализации случайного события - вероятность. Вероятность есть объективная мера возможности наступления события независимо от того, является ли оно массовым или нет. В жизни все (полуинтуитивно) применяют вероятностные оценки будущим событиям и весьма успешно.

Частота события А (статистическая вероятность).

,

где - число опытов, в которых наблюдается событие А;

n - общее число опытов.

Значения  - случайны.

,

где  - математическая вероятность, являющаяся достоверной величиной, т.е. вероятность того, что при n®¥  равна 1.

.

При   вероятность  , при  соответственно .

События несовместны в данном испытании, если никакие два из них не могут появиться вместе. (Например, появление цифр от 1 до 6 на игральном кубике).

Случайные события совместны, если при данном испытании могут произойти два эти события.

Если события А и В несовместны, то вероятность появления или события А или события В:

                                  (1.2)

или в общем виде                                                            (1'.2).

Сумма вероятностей двух противоположных событий

                                                                          (2.2).

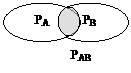Событие А независимо от В, если вероятность появления события А не зависит от того, произошло событие В или нет.

Если события А и В независимы (они совместны), то вероятность появления и события А и события В равна:

           ,                                             (3.2).

В урне два кубика – черный и белый и два шарика – черный и белый. Вероятность появления черного кубика равна произведению вероятностей появления черного цвета и кубика, т.е. 1/2×1/2=1/4.

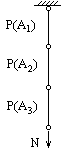Из формулы (3.2) видно, например, что если событие А (появление максимальной ветровой нагрузки) и событие В (появление максимальной снеговой нагрузки) – независимы, то вероятность одновременного появления А и В (т.е. максимумов нагрузок) меньше вероятности появления одного из событий (максимумов нагрузки) .

Это учитывается коэффициентом сочетаний y.

Вероятность  тем меньше, чем меньше  и .

Формула (3¢.2) иллюстрируется последовательным соединением. Вероятность неразрушения последовательной системы:

,                                                               (4.2)

где , i =1,3 – вероятности неразрушения i‑го элемента системы,

 – событие, состоящее в неразрушении  i–го элемента системы.

Пример последовательного соединения: статически определимая система т.к. разрушение всей системы происходит при разрушении хотя бы одного из элементов, т.о. вероятность неразрушения всей системы меньше вероятности неразрушения любого ее отдельного элемента.

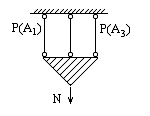Формула (3.2) также иллюстрируется и параллельным соединением. Вероятность разрушения параллельной системы:

,                                             (4'.2)

где  – вероятности разрушения i–го элемента системы.

Вероятность неразрушения параллельной системы:

                          (5.2)

или в общем виде:                                                                                       (5'.2).

Пример параллельного соединения: статически неопределимая система т.к. разрушение всей системы происходит при разрушении всех избыточных и еще одной связей. Т.о. вероятность неразрушения всей системы больше вероятности неразрушения любого ее отдельного элемента. Однако в действительности в статически неопределимой системе вероятности разрушения элементов системы не независимы, т.к. разрушение одного элемента из-за перераспределения усилий приводит к изменению вероятностей разрушения остальных элементов.

Например, при диаграмме Прандтля «условное» разрушение одного элемента статически неопределимой системы (т.е. напряжение в этом элементе при увеличении N остается постоянным и равным ) в меньшей степени приводит к перераспределению усилий, а, следовательно, и к изменению вероятностей разрушения. Т.о. статически неопределимая система со стержнями, работающими по диаграмме Прандтля, больше подходит в качестве примера для параллельной системы.

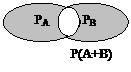Если случайные события А и В совместны (и независимы), то вероятность появления или А или В:

  (6),       (6.2).

Если случайные события А и В зависимы (и совместны) и вероятности их появления Р(А) и Р(В), то вероятность совмещения событий А и В (произойдет и А и В):

                                                                   (7.2),

где  – условная вероятность, т.е. вероятность появления события В, при условии, что событие А произошло. Аналогично                                                         (7¢.2).

Например, в урне два черных и два белых шара. Событие А – появление белого шара с первого раза, событие В - появление белого шара со второго раза. Вероятность появления белого шара два раза подряд определяется формулой:

Р(АВ)=Р(А)Р(ВА)=1/2·1/3=1/6.

Из формул (7) и (7¢) можно получить:

                                                                  (8.2),

где  – априорная вероятность появления события А, определенная до того как стала известна информация о событии В.

 – апостериорная вероятность появления события А, основанная на этой информации. А и В произошли, но мы определяем вероятность того, что перед В было А.

Если А и В независимы, то  и наоборот.

Пусть имеется n несовместных событий  с вероятностями их появления  и пусть  – условные вероятности осуществления события В с одним из n событий . (Т.е. события В и А1, В и А2,…, В и Аn – зависимы и совместны). Тогда вероятность осуществления события В:

                                                              (9.2)

Это формула полной вероятности,

где  - вероятность того, что произойдет В и ;

 – по другому – вероятность того, что В произойдет с любым из .

Пусть событие В произошло, это изменит вероятности . Надо найти условные вероятности  осуществления события , i =1,…n при условии, что В произошло (т.е. если В произошло, то надо найти вероятность того, что ему предшествовало появление именно события ).

Формула полной вероятности Байеса (из (9) и (8)):

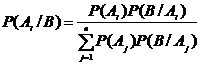                                                         (10.2),

где  – вероятность появления события  до того как произошло В;

i =1, 2,…n.

( – как бы является удельным весом вероятности  в сумме всех вероятностей ).

Производится n независимых опытов, имеющих два возможных исхода – появление и непоявление события А (вероятность появления p , непоявления q = 1 - p). Вероятность того, что при n испытаниях событие А наступает m  раз:

(формула Бернулли):

                                                          (11.2),

где  - число сочетаний из m элементов в n.

Пример: ;

.

Вероятность  того, что в результате n независимых опытов событие А произойдет хотя бы один раз (может и больше): Рn(A) = 1 - qn,

где q - вероятность непоявления события А в первом испытании;

qn - вероятность того, что А не произойдет ни разу;

1 - qn - вероятность того, что А произойдет один раз, или два раза ... или все n раз.

Пример. Событие А - разрушение здания в сейсмическом районе, p = 0,1 - вероятность разрушения его в течение первого года. Тогда q =1 - p - вероятность неразрушения в течение первого. Тогда Р2(А)=1-0.92=0.19, Р3(А)=1-0.93=0.271, Р10(А)=1-0.910=0.651, Р20(А)=1-0.920=0.878, Р50(А)=1-0.950=0.995, где Pn(A) – вероятности разрушения здания за n лет.

Т.о. функция надежности (зависимость вероятности неразрушения от пройденного количества лет) от значения 1 асимптотически приближается к ОХ.