Случайная векторная величина двух измерений

На практике решаются задачи, в которых результат опыта описывается не одной с.в., а двумя или более с.в., образующими систему. При этом свойства системы нескольких с.в. могут включать и взаимные связи (зависимости) между ними.

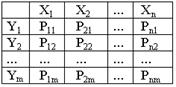Если с.в. X и Y принимают дискретные значения xi, yj и каждой паре значений (xi, yj) соответствует определенная вероятность pij, то можно составить таблицу распределения вероятностей дискретной двумерной с.в.

Очевидно .

Значение функции Р(x,y) равно вероятности обнаружить с.в. Х<х и с.в. Y<y, т.е.

P(x,y)=Prob(X<x,Y<y).

Свойства функции распределения Р(x,y):

1) Р(х,y) - неубывающая функция своих аргументов,

т.е. при х2>x1 P(x2,y)>P(x1,y) или при y2>y1 P(x,y2)>P(x,y1);

2) P(x,-¥)=P(-¥,y)=P(-¥,-¥)=0;

3) P(x,+¥)=P(x), P(+¥,y)=P(y) - если один из аргументов равен +¥, то функция распределения Р(х,y) превращается в функцию распределения другой с.в.;

4) P(+¥,+¥)=1.

Плотность распределения системы двух с.в. (вторая смешанная производная P(x,y) по  и затем по ).

                                                  (25.3)º(15.3)

или в общем виде

, .

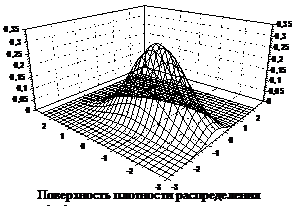
Геометрически p(x,y) можно представить поверхностью (поверхность распределения - по ОХ и OY откладываются значения с.в. X и Y, по Z - вероятность их появления, см. рис.  ).

Из (25) следует

                                                  (26.3)º(17.3).

Вероятность обнаружить двумерную с.в. (X,Y) в области D:

Prob((X,Y)ÌD)=                                        (27.3)=(16.3).

Вероятность обнаружить точку М с координатами х1, х2,...хn в n-мерном объеме V:

Prob(MÌV)=                                (27¢.3)

Далее, аналогично (18)

                                                              (28.3),

т.е. геометрически объем под поверхностью распределения равен 1.

В общем виде имеем n-кратный интеграл

                                            (28¢.3).

Если известен закон распределения системы двух случайных величин p(x,y), то можно определить законы распределения отдельных величин, входящих в систему:

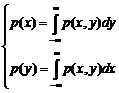                                                                      (29.3).

То же, в общем виде:

                              (29¢.3).

Но для того, чтобы по заданным законам распределения отдельных с.в., входящих в систему, определить законы распределения системы с.в., надо знать зависимость между величинами, входящими в систему.

Условный закон распределения с.в. Х, входящей в систему (X,Y) - закон ее распределения, вычисленный при условии, что другая с.в. Y приняла определенное значение. Условный закон распределения можно задавать функцией P(x/y) и плотностью p(x/y) распределения.

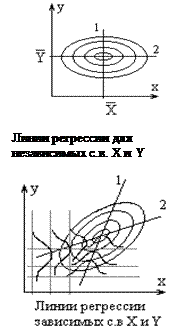
Геометрически функция плотности распределения p(x/y) представляет собой сечение поверхности распределения при y=const. Сечения поверхности распределения плоскостями x=const и y=const дают соответственно условные плотности распределения p(y/x) величины Y при определенных значениях x и условные плотности распределения p(x/y) величины X при определенных значениях y. Если X и Y - зависимые с.в., то кривые плотности распределения p(y/x) изменяются при изменении x, а кривые плотности распределения p(x/y) изменяются при изменении y. М.о. этих кривых при таких изменениях образуют линии регрессии 1 и 2. В случае независимости X и Y линии регрессии представляют собой прямые  и , параллельные осям координат. При наличии функциональной связи (а не стохастической) между X и Y обе линии регрессии сливаются в одну - y=y(x), при этом поверхность плотности распределения может быть заменена кривой плотности распределения X или Y вдоль линии y=y(x).

С учетом вышесказанного плотность распределения системы двух с.в. равна плотности распределения одной из них, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение:

p(x,y)=p(x)p(y/x)                                                         (30.3)=(7.2)

или в общем случае

p(x1,x2,...,xn)=p(x1,x2,...,xi/xi+1,xi+2,...,xn)p(xi+1,xi+2,...,xn)                               (30¢.3).

Для независимых с.в. p(x,y)=p(x)p(y)  (31)=(3) - плотность распределения системы независимых с.в. равна произведению плотностей распределения отдельных величин, входящих в систему.