Формулировка и математическое выражение второго начала термодинамики

Установление второго начала термодинамики связано сисследованиями французского военного инженера С. Карно (1824 г.) принципов действия тепловых двигателей, т.е. машин, превращающих теплоту в работу, с целью повышения их коэффициента полезного действия (КПД). Окончательно второе начало термодинамики было сформулировано Р. Клаузиусом в 1850 году и У. Томпсоном (лордом Кельвином) в 1851 году.

Существует несколько эквивалентных формулировок второго начала термодинамики:

1. Невозможен самопроизвольный переход тепла от тела менее нагретого к телу более нагретому (Р. Клаузис).

2. Невозможно превратить теплоту в работу, не производя никакого другого действия, кроме охлаждения источника тепла (У. Томпсон, М. Планк).

3. Вечный двигатель второго рода невозможен (В. Оствальд).

Вечным двигателем второго рода называют такую машину, единственным результатом действия которой было бы получение работы за счет теплоты окружающей среды.

В любой системе два произвольно выбранные состояния (1” и 2”) различаются тем, что процесс перехода из состояния 1 в состояние 2 протекает самопроизвольно, а обратный процесс перехода из состояния 2 в состояние 1 самопроизвольно не идет.

Отсюда можно заключить, что существует какой-то объективный критерий, позволяющий установить принципиальное различие между этими двумя состояниями системы.

Рассмотрим изолированную систему, состоящую из теплового резервуара, 1 моля идеального газа, заключенного в цилиндре с подвижным поршнем, и устройства, позволяющего за счет перемещения поршня совершать работу (рис. 3.2).

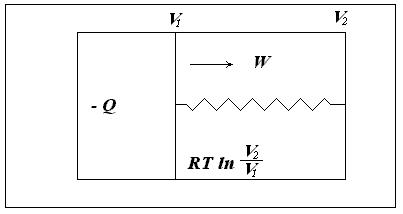
Рис. 3.2. Изолированная система, состоящая из теплового резервуара, 1 моля идеального газа, заключенного в цилиндре с подвижным поршнем, и устройства, позволяющего за счет перемещения поршня совершать работу

Предположим, что газ обратимо расширяется от объема V1 до V2 и совершает работу W1. Энергия на совершение работы передается в форме тепла из резервуара. совершаемая газом работа равна полученной от резервуара энергии Q1:

.                                                                                                     (3.8)

Функция  определяется не только изменением объема, но и температурой. Разделим обе части уравнения на Т:

.                                                                                                                     (3.9)

Из равенства (3.9) видно, что изменения, происходящие в изолированной системе при протекании обратимого процесса, могут быть охарактеризованы величиной , которая определяется только исходным (V1) и конечным (V2) состоянием системы. Увеличение параметра  в цилиндре с газом эквивалентно уменьшению этого параметра для теплового резервуара , т.е.

.                                                                                                             (3.10)

При необратимом (самопроизвольном) расширении идеального газа от V1 до V2 (например, в вакууме, рис. 3.3) процесс происходит без совершения газом работы, так как Р=О и, соответственно, передача энергии от резервуара не происходит: Q=0, т.е. изменение внутренней энергии (DU) для газа равно нулю.

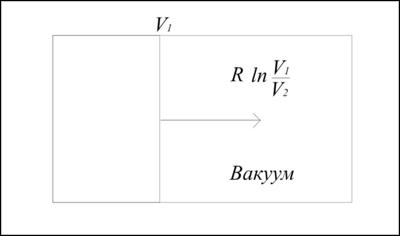
Рис. 3.3. При самопроизвольном расширении идеального газа от V1 до V2 в вакууме процесс происходит без совершения газом работы, так как Р = О и,
соответственно, передачи энергии от резервуара не происходит: Q = 0,
т.е. изменение внутренней энергии (D U) для газа равно нулю

Однако состояние газа в резервуаре изменилось на величину , а состояние резервуара – нет. Поэтому в целом состояние системы изменилось на величину , т.е. , так как

.                                                                                                                               (3.11)

Таким образом, протекание самопроизвольного процесса в изолированной системе в общем случае связано с возрастанием некоего параметра состояния системы. Этот параметр получил название энтропии.

Из примера следует, что самопроизвольно в изолированной системе протекают те процессы, которые приводят к возрастанию энтропии системы.

Если энтропия системы в исходном состоянии может быть выражена как S1 = R ln V1, а в конечном состоянии S2 = R ln V2, то изменение энтропии в результате протекания обратимого процесса следующее:

DS = S2 - S1 = R ln V2/V1,

или

DS(обр.процесс) = .                                                                                                   (3.12)

Соответственно для необратимого процесса (самопроизвольного)

DS(необр.процесс) > .                                                                                            (3.13)

Справедливость последнего выражения следует из первого начала термодинамики.

В соответствии с I началом:

DU = Q – W.                                                                                                                            (3.14)

Переведем систему из состояния 1 в состояние 2 обратимым и необратимым путем:

DU(обр)=Qобр – Wобр,                                                                                                         (3.15)

DU(необр) = Qнеобр – Wнеобр.                                                                                          (3.16)

Если DU является функцией состояния, то DU(обр) = DU(необр). Известно, что Wобр > Wнеобр, следовательно Qобр > Qнеобр. DS не зависит от пути процесса, так как является функцией состояния, т.е. DS(обр) = DS(необр). Тогда

                                                                                                      (3.17)

или в общем случае

;                                                                                                                             (3.18)

.                                                                                                                           (3.19)

Знак равенства относится к обратимым, неравенства – к необратимым процессам.