Уравнение Клаузиуса-Клапейрона

Из рис. 6.1 видно, что наклон ВО и ОА награфике задается производной dp/dT, которая представляет собой скорость изменения давления пара от Т. Наклон ОС численно равен dp/dT – величина, обратная скорости, с которой точка плавления изменяется при изменении давления. Уравнение, которое связывает эти изменения с другими измеряемыми свойствами системы, было предложено в 1834 году Б. Клапейроном и позже модифицировано Р. Клаузиусом.

Это уравнение можно вывести, используя термодинамические соотношения для химического потенциала. В принципе любые свойства (такие, как объем, энтальпия, свободная энергия) зависят от количества вещества и являются экстенсивными. Однако если они относятся к одному молю вещества в строго определенных условиях, они становятся характеристичными свойствами вещества при данных условиях.

Объем, реально занимаемый одним молем растворенного вещества, называется парциальным молярным объемом растворенного вещества. Он соответствует изменению общего объема очень большого количества раствора при добавлении одного моля растворенного вещества. Очевидно, что при добавлении одного моля растворенного вещества концентрация не будет меняться только при условии бесконечно большого объема исходного раствора.

В этом случае для парциального объема можно записать:

,

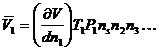где V – общий объем раствора, Т – температура, Р –давление, n – число молей других веществ. Величина V является функцией Т и Р, а также состава раствора.

Если компонент распределен между двумя фазами a и b, то при равновесии ma=mb. В случае однокомпонентной системы химический потенциал равен величине свободной энергии, приходящейся на 1 моль: ma = `G a и mb = `Gb.

Если ma будет слегка меняться при небольших изменениях Т и Р, то аналогичное изменение будет наблюдаться и для mb (при сохранении равновесия). Поэтому можно записать .

Далее мы знаем, что

dG = Vdp-SdT.                                                                                                                       (6.4.)

Подставим в это уравнение выражение для парциальных молярных величин

adp - `S adT = `Vbdp - `S bdT.                                                                                     (6.5)

Преобразуем выражение (6.5) в виде члена dp/dT

.                                                                                              (6.6)

Выражение DS по второму началу термодинамики , где Qобр представляет собой молярную теплоту испарения или молярную теплоту плавления.

Подставим DS в уравнение (6.6) и получим уравнение Клапейрона:

.                                                                                                                      (6.7)

В таком виде это уравнение нельзя проинтегрировать. Р. Клаузиус предложил несколько допущений, что позволяет преобразовывать уравнение в более удобную форму – например, в случае равновесия пар – вода  равно (). Величина `Vж для воды составляет приблизительно 0,1% от `Vг и поэтому `Vж можно не учитывать в члене `V(г) – `V(ж). Тогда придем к уравнению

.                                                                                                                   (6.8)

Если принять, что пар подчиняется законам идеального газа, то вместо  запишем RT / P:

.

Заменим выражение для Q более традиционным DНV, получим уравнение Клаузиуса-Клапейрона в обычной форме:

.                                                                                                                  (6.9)

Это уравнение можно проинтегрировать, если предположить, что молярная теплота испарения DНV является постоянной, т.е. не зависит от температуры. После интегрирования в пределах между Р1, Т1 и Р2, Т2 получаем:

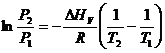
или в форме

.                                                                                                 (6.10)