Основы финансовой математики

Как уже упоминалось выше, при выполнении своих функций финансовый менеджмент руководствуется рядом концепций, одной из которых является концепция временной оценки денег утверждающая, что денежная единица, полученная сегодня, и денежная единица, ожидаемая к получению в будущем, не равноценны. Причины этого предположения:

• имеющиеся сейчас деньги можно инвестировать, получить доход, в результате чего денег станет больше;
• под действием инфляции покупательная способность денег снижается;
• всегда существует риск не получить всей суммы денег в будущем.

Простейшим видом финансовой сделки является однократный заём суммы  с условием, что через некоторое время t будет возвращена сумма . Результативность этой сделки характеризуется специальным коэффициентом – ставкой.

В финансовых вычислениях показатель  называют процентная ставка, норма прибыли, доходность, а  – учетная ставка, ставка дисконтирования, дисконт. Это показатели взаимосвязаны и выражаются в процентах или долях единицы.

Наращение – процесс, в котором задана исходная сумма и ставка в финансовых вычислениях. В данном случае, искомая величина называется наращенной суммой, используемая ставка – ставкой наращения, а денежный поток движется от настоящего к будущему.

Дисконтирование – процесс, в котором задана сумма, ожидаемая к получению в будущем, и ставка. В данном случае, искомая величина будет называться приведенной суммой, ставка – ставкой дисконтирования, а денежный поток движется от будущего к настоящему.

Предоставляя деньги в долг, их владелец получает доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Наиболее распространен вариант, когда ставка процента устанавливается в виде годовой ставки и подразумевается однократное начисление процентов по истечении года со дня получения ссуды. Существуют два алгоритма начисления:

• схема простых процентов ;
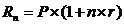• схема сложных процентов .

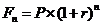Для кредитора более выгодной является схема простых процентов, если срок ссуды менее одного года, а проценты начисляются единожды в конце периода, если же срок превышает один год и проценты начисляются ежегодно, то более выгодной становится схема сложных процентов.

При начислении процентов за дробное число лет используется смешанная схема, т.е. схема сложных процентов для целого числа лет и схема простых процентов – для дробной части.

Функция сложных процентов является одной из базовых в финансовом менеджменте. Поэтому для удобства используют значения множителя FM1(r, n), называемого мультиплицирующим множителем для единичного платежа.  Экономический смысл этого множителя в том, что он показывает величину денежной единицы через n периодов при заданной процентной ставке.

На практике многие финансовые операции выполняются в рамках одного года, при этом могут использоваться различные схемы и методы начисления процентов. Большое распространение имеют краткосрочные ссуды на срок до одного года с однократным начислением процентов. В этом случае, для кредитора, диктующего условия финансового контракта более выгодна схема простых процентов. При этом в расчетах используют промежуточную процентную ставку, которая равна доле годовой ставки пропорциональной временному интервалу в году.

 – годовая ставка процента,  – продолжительность операции в днях,  – продолжительность года в днях.

Определяя продолжительность финансовой операции, принято день выдачи и день погашения ссуды считать одним днем. Размер промежуточной процентной ставки может быть различным, в зависимости от продолжительности года, квартала, месяца. Возможны 2 варианта:

• Точный процент, определяемый исходя из продолжительности в 365/366 дней в году, 89-92 дней в квартале, 28-31 дней в месяце;
• Обыкновенный процент, определяемый исходя из приближенного числа дней в году, квартале, месяце (360, 90, 30 соответственно).

Другой распространенной операцией краткосрочного характера, для оценки которой используются рассмотренные формулы, является операция по учету векселей банком. В этом случае пользуются ставкой дисконта. Одна из причин в том, что чаще всего банку приходится иметь дело с суммой к погашению, то есть величиной FV. Схема действия, в этом случае, следующая: владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его (купить), удерживая в свою пользу часть вексельной суммы, которая называется дисконтом. В этом случае банк предлагает владельцу сумму PV, исчисляемую исходя из объявленной банком учетной ставки d. Чем выше ее значение, тем большую сумму удерживает банк в свою пользу. Расчет проводится по следующей формуле:

Разность между  (номинальной величиной векселя) и  (дисконтированной величиной векселя) представляет собой комиссионные банка за предоставленную услугу.

Все рассмотренные ранее начисляемые проценты – дискретные, т.к.  начисление осуществляется за фиксированный промежуток времени (год, квартал, месяц). Уменьшая этот промежуток и увеличивая частоту начисления в пределе можно перейти к непрерывным процентам. Ставку непрерывных процентов обозначают  (дельта) и называют силой роста. Формула для нахождения суммы за n лет при непрерывном начислении процентов принимает вид:

 – число Эйлера,  = 2,718281

Оценивая целесообразность финансовых вложений, тот или иной вид бизнеса исходит из того, является ли это вложение более прибыльным при допустимом уровне риска, чем вложение в государственные ценные бумаги. Используя ряд методов можно проанализировать будущие доходы при минимальном безопасном уровне доходности. Основная идея этих методов заключается в оценке будущих поступлений (Fn) с позиции текущего момента. При этом сделав финансовое вложение инвестор обычно руководствуется тремя условиями:

• Происходит постоянное обесценение денег.
• Темп изменений цен на сырье, материалы и основные средства может существенно отличаться от темпа инфляции;
• Желательно периодическое начисление дохода в размере не ниже определенного уровня.

Базовая расчетная формула для такого анализа имеет вид:

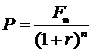
 – доход, планируемый к поступлению в n-ом году,  – текущая (приведенная) стоимость или оценка величины  с позиции текущего момента,  – ставка дисконтирования.

Для упрощения расчета, в финансовом менеджменте применяют дисконтирующий сомножитель FM2(r, n). Его экономический смысл в том, что он показывает сегодняшнюю цену одной денежной единицы будущего при заданной процентной ставке и величине периода.

Определяя ставку дисконтирования, исходят из гарантированного инвестиционного уровня доходности, который обеспечивается банком по вкладам или при операциях с ценными бумагами. При этом может присутствовать надбавка за риск, размер которой пропорционален уровню риска проекта.

Различными видами финансовых контрактов могут предусматриваться разные схемы начисления процентов, причем, обычно, в данном случае оговаривается годовая номинальная процентная ставка, которая  не отражает реальной эффективности сделки и не может использоваться для сопоставлений.

Ввиду того, что частота начислений может быть различной, очень важно знать способ сравнения процентных ставок. Это делается путем вычисления действующей или эффективной годовой процентной ставки, которую можно определить по формуле:

 - номинальная процентная ставка, указанная в контракте, - эффективная ставка, - число начислений процентов за период.

Одним из основных элементов финансового анализа является оценка денежного потока , , … , , генерируемого в течение ряда временных периодов в результате реализации какого-либо проекта или функционирования какого-либо вида активов. Элементы потока  могут быть независимыми или связанными между собой определенным алгоритмом. Предполагается, что временные периоды равны, а также то, что элементы денежного потока являются однонаправленными, то есть, нет оттоков и притоков денежных средств.

Считается, что генерируемые в рамках одного временного периода поступления  имеют место либо в его начале. Другими словами они распределены не внутри периода, а сконцентрированы на одной из его границ. В данном случае, при авансовом характере денежного потока он называется prenumerando, а при постоплатном – postnumerando.

Оценка денежного потока может выполняться в рамках решения двух задач:

• Прямой, когда оценка проводится с позиции будущего, т.е. реализуется схема наращения.
• Обратной, когда оценка проводится с позиции настоящего, т.е. реализуется схема дисконтирования.

 Прямая задача предполагает суммарную оценку наращенного денежного потока. В ее основе лежит будущая стоимость. В частности, если денежный поток представляет собой регулярное начисление процентов на вложенный капитал () по схеме сложных процентов, то в основе суммарной оценки наращенного денежного потока лежит формула:

Обратная задача предполагает суммарную оценку дисконтированного денежного потока, поскольку отдельные элементы денежного потока генерируются в различные временные интервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Приведение денежного потока к одному моменту времени осуществляется с помощью формулы:

Основным результатом расчета является определение общей величины приведенного денежного потока. Используемые при этом формулы различаются в зависимости от вида потока: postnumerando или prenumerando.

Ситуация, когда денежные поступления по годам варьируют, является наиболее распространенной, общая постановка задачи в данном случае такова: для денежного потока , , … ,  необходимо найти стоимость с позиции будущего (прямая задача) и с позиции настоящего (обратная задача) при заданной ставке .

Для потока postnumerando прямая задача предполагает оценку на конец n-ного периода, когда реализуется схема наращения. На первое денежное поступление  начисляются проценты по формуле , на второе денежное поступление , на предпоследнее поступление , а на последнее поступление начисления не производится. Тогда наращенный денежный поток примет вид:

,, …, , ,

Будущая стоимость  исходного денежного потока представляет собой сумму наращенных поступлений:

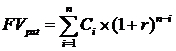
Обратная задача потока postnumerando подразумевает оценку с позиции текущего момента, т.е. на конец периода, когда реализуется схема дисконтирования и расчеты необходимо вести по приведенному потоку. Элементы приведенного потока можно суммировать, а их сумма характеризует текущую стоимость денежного потока, которую можно сравнить с величиной первоначальных инвестиций.

Приведенный денежный поток postnumerando имеет вид:

, , …,

Приведенная стоимость  определяется формулой:

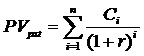
Для денежных потоков prenumerando логика расчета остается прежней, однако формулы принимают следующий вид:

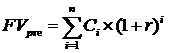
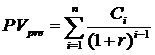
Аннуитет – частный случай денежного потока, к определению которого есть 2 подхода:

• аннуитет – однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы;
• аннуитет – однонаправленный денежный поток, элементы которого одинаковы по величине и имеют место через равные временные интервалы.

Если число равных временных интервалов ограничено, аннуитет называют срочным. Аннуитеты также разделяются на postnumerando и prenumerando.

Для оценки будущей и приведенной стоимости аннуитетов используются те же формулы, что и для других денежных потоков postnumerando и prenumerando. Однако, ввиду специфики аннуитетов, для упрощения расчетов были выведены множители FM3(r, n) и FM4(r, n). Тогда формулы приобретают вид: