Для идеальных газов уравнение Клапейрона: 
. Для реальных газов оно соблюдается лишь приближенно. Отступления от идеальной модели связаны с наличием жидкого и твердого состояний и наличием межмолекулярного взаимодействия.
Потенциал взаимодействия (Леннарда-Джонса): 
.
Здесь 
– константы, 
– расстояние между центрами взаимодействующих частиц. Этот потенциал с хорошей точностью описывает реальный газ. На рисунке 1 
– диаметр молекулы. Рассматриваемая модель газа: твердые упруго сталкивающиеся шары, причем возможны только парные столкновения (это выполняется довольно точно при небольших давлениях газа).
Уравнение Ван-дер-Ваальса 
,
где 
– универсальная газовая постоянная, 
– давление, 
– объем, 
– температура, 
– поправка на то, что отдельно взятой молекуле предоставлен не весь объем , т.к. молекулы не могут сблизиться на расстояние, меньшее ; 
– поправка на то, что на пристеночный слой газа действует сила со стороны всего газа, стремящаяся втянуть внутрь газа пристеночный слой.
– так называемое внутреннее давление.
или 
,
где 
– концентрация, 
– масса частицы, – скорость частицы. Для можно получить:
.
Теоретический вывод уравнения Ван-Дер-Ваальса применим при условях:
.
В случае плотных газов уравнение Ван-Дер-Ваальса лишь качественно описывает поведение газа. Для реальных газов 
и зависят от температуры.
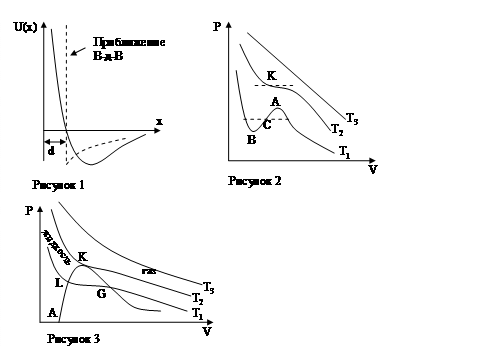
Изотермы Ван-Дер-Ваальса (рисунок 2).
. Здесь при 
наблюдается критическая изотерма, т.е. при 
уравнение изотермы имеет один корень при 
. Точка 
называется критической.
, 
, 
.
Уравнение изотермы:
Участки типа ВСА соответствуют неустойчивому состоянию вещества и практически не могут быть реализованы.
Изотермы реального газа (рисунок 3).
Область между кривой ALKG и изобарой 
соответствует двухфазным состояниям вещества, т.е. каждая точка этой области изображает такое состояние вещества, в котором оно не является физически однородным, а состоит из жидкости и ее насыщенного пара (за исключением случаев неустойчивого состояния в виде перегретой жидкости или пересыщенного пара).
Поможем написать любую работу на аналогичную тему