Для описания микрочастицы необходимо, чтобы были определены:
1) величины, задающие состояние частицы;
2) уравнение движения, определяющее изменение состояния частицы;
3) физические величины, доступные измерению и способ получения их значений в данном состоянии.
Для микрочастиц из-за соотношений неопределенности классическое определение состояния (координата и импульс, а следовательно и сила) не подойдет. В соответствии с корпускулярно-волновым дуализма в квантовой теории состояния частицы задается волновая функция 
, которая является комплексной величиной и формально обладает волновыми свойствами. Для волновой функции характерны следующие свойства:
1) с помощью волновой функции определяется вероятность 
(7), то есть вероятность нахождения частицы в единице объема 
2) волновая функция нормирована на единицу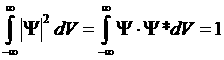 
(8), то есть, во всем пространстве, где волновая функция отлична от нуля, частица может быть достоверно найдена
3) для волновых функций имеет место принцип суперпозиции 
что объясняет проявление волновых свойств частицы
4) так как волновая функция описывает реальные частицы, она должна быть конечной, непрерывной, гладкой и однозначно определяемой.
Рассмотрим свободную частицу, способную двигаться вдоль оси x в отсутствии внешних полей. Такая частица должна описываться плоской волной 
(9) или, учитывая связь волнового числа и импульса 
, а также частоты и энергии 
, тогда выражение (9) примет вид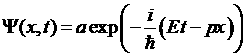 
(10).
Продифференцируем (10) по времени и по координате:
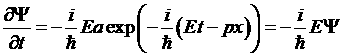(11)
; 
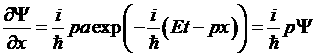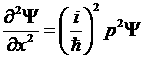(12)
Учитывая связь энергии и импульса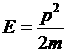 
для свободной частицы и следствия уравнений (11) и (12) 
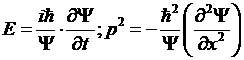, получим одномерное уравнение 
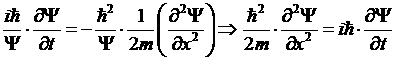(13).
В общем случаи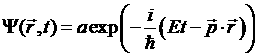 
и в левой части берется сумма производных по координатам.
Последнее уравнение может быть записано, используя операторную форму. Вводя оператор полной энергии частицы – оператор Гамильтона - сумму операторов кинетической и потенциальной энергии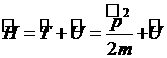 
(14) и оператор импульса 
, в декартовых координатах он примет вид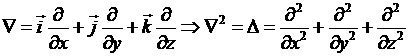 
, в одномерном случаи 
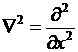. Действие оператора потенциальной энергии сводится к его домножению на волновую функцию поэтому выражение (13) примет вид: 
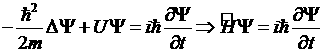(14) – временное уравнение Шредингера.
В случаи, когда потенциальная энергия частицы не зависит от времени волновую функцию можно представить как произведение чисто временной и чисто координатной частей 
, тогда переменные в (14) разделяются и задача сводится к нахождению собственных функций и собственных значений оператора Гамильтона 
(15) –стационарное уравнение Шредингера. Решая уравнение Шредингера находят волновую функцию и плотность вероятности положения частицы в пространстве.
Поможем написать любую работу на аналогичную тему