Неполярные диэлектрики.

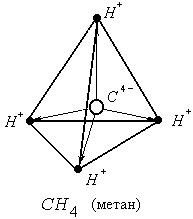
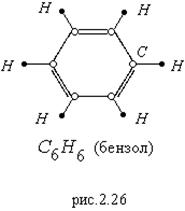
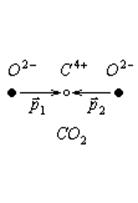
Этот тип диэлектриков имеет структуру, при которой у каждой молекулы  при . Представители – N2, CO2, C6H6, CH4 (рис.2.26). Из рис. ясно, что симметрия молекул такова, что дипольный момент в них не возникает при .

При  положительные заряды смещаются вдоль , а отрицательные – против. В результате появляется момент .

,                                        (2.79)

где - молекулярная восприимчивость. Общая поляризация на единицу объема:

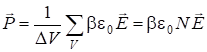,                         (2.80)

где  - число молекул в единице объема. Поскольку , то , где  - восприимчивость единицы объема, ;

             -                  (2.81)

диэлектрическая проницаемость.

          Для оценки  воспользуемся моделью молекулы в виде проводящей сферы радиуса . Во внешнем электрическом поле  сфера приобретает дипольный момент, так как  и  заряды смещаются.

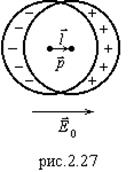          Используя модель двух шаров одинакового радиуса с одинаковой объемной плотностью зарядов  и , сдвинутых на  (см. рис.2.27), по теореме Гаусса получим поле внутри шара в любой точке:

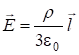.                      (2.82)

          Заряды, не равные нулю, есть лишь на пересекающихся серповидных частях шаров. Момент полученного диполя:

.

Так как , то с учетом (2.82) получим:

.         (2.83)

Тогда:

.                                      (2.84)

При            ,          ,

.                          (2.85)

Видно, что . При           ,   .

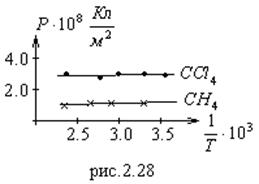          Модель применима для газов, в которых молекулы не взаимодействуют. Сравним результа-ты расчета с экспериментом. На рис.2.28 приведена зависимость поляризуемости от обратной температуры четырех-хлористого углерода СCl4 и метана СН4. Видно, что зависимость от температуры поляризуемости для этих неполярных газов отсутствует.