Полярные диэлектрики.

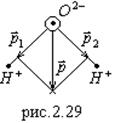
Для полярных диэлектриков каждая молекула имеет  при . Принадлежность к полярным диэлектрикам связана с симметрией молекул. Пример: СО, Н2О (рис.2.29): .

      Так как энергия диполя в электрическом поле (2.59):

,

то минимуму энергии отвечает ориентация . Такой ориентации препятствует тепловое движение. Если рассматривать не одну молекулу, а много невзаимодействующих молекул, то тепловое движение создает при  из-за хаотической ориентации дипольных моментов молекул.

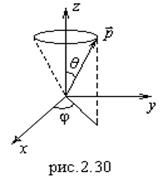          Для расчета восприимчивости воспользуемся моделью идеального газа дипольных моментов, т.е. не будем учитывать взаимодействие моментов между собой. Направим  вдоль оси  (рис.2.30). Возможны разные ориентации  относительно  из-за конкуренции двух энергий: энергии поля и тепловой.

          Распределение ориентации  относительно  - это распределение по углам . Считаем, что оно подчиняется статистике Больцмана.

Число моментов в телесном угле :

.                                      (2.86)

Среднее значение компоненты дипольного момента на оси z : ;

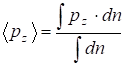.                                (2.87)

Введем статинтеграл:

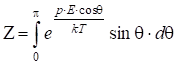,                               (2.88)

тогда

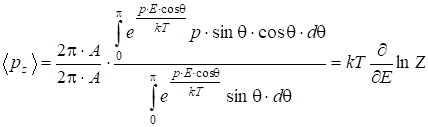.   (2.89)

          Задача сводится к расчету , т.е. интеграла (2.88). Обозначим :

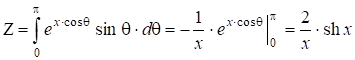;         (2.90)

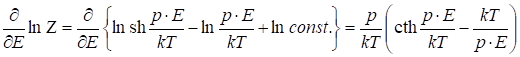.  (2.91)

Подстановка в (2.89) дает:

,                                 (2.92)

где  - функция Ланжевена.

.                             (2.93)

Рассмотрим предельные значения .

1.  - слабые поля; т.е.  Подставив приближенное выражение в (2.92), имеем: 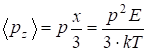. При учете  получаем зависимость восприимчивости от температуры в виде:

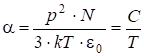,                                    (2.94)

носящую название закона Кюри.

2.  - сильные поля: . Из (2.92) получаем: .

                                  (2.95).

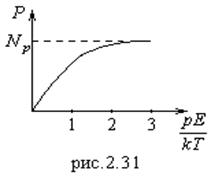Видно, что все моменты  ориентированы вдоль . Зависимость (2.92) приведена в общем виде на рис.2.31. Оценим величину поля, при котором . Если:

 ;

то    .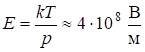

Много ли это?

Возьмем конденсатор с расстояниями между пластинами  и разность потенциалов 2 кВ. Напряженность поля в нем . Полученное значение поля на три порядка меньше, чем рассчитанная выше величина сильного поля.

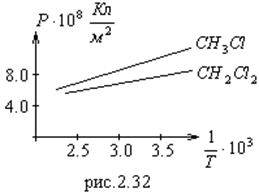Сравним полученные теорети-ческие результаты с экспериментом. На рис.2.32 приведена зависимость поляризуемости от Т-1 для замещенного метана. Видно, что выполняется закон Кюри (2.94).