Электродвижущая сила. Правила Кирхгофа.

Закон Ома для замкнутого проводника или для электрической цепи можно вывести, используя выражения (5.5), (5.12). Возьмем замкнутый проводник, элемент длины которого . Тогда:

;

Используем то, что сила тока, или просто ток, . Тогда:

.

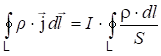Таким образом:

;                               (5.17)

          или             .

Это закон Ома для замкнутого проводника. Здесь  - полное сопротивление всей цепи. Так как для электростатического поля  то для того, чтобы ЭДС было отлично от нуля , нужны сторонние непотенциальные источники электрического поля.

          Из (5.17) следует определение :

ЭДС – это работа сторонних сил по перемещению единичного положительного заряда вдоль замкнутого проводника.

Если участок цепи не содержит источника, то закон Ома принимает вид:

,                                 (5.18)

где  - разность потенциалов на этом участке цепи.

          Применим закон Ома для изучения последовательного и параллельного соединения проводников.

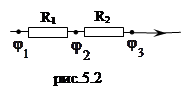1. Случай последовательного соединения проводников (рис.5.2). Используя (5.18), запишем для каждого проводника:

.

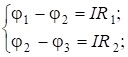
Таким образом, для последовательного сопротивления проводников:

.                                         (5.19)

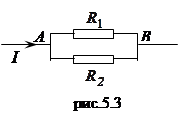2. Случай параллельного соединения проводников (рис.5.3). Для точки А можно записать:

;

Тогда по (5.19):

         .

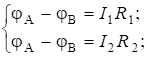
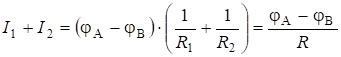Значит, при параллельном соединения проводников:

.                                   (5.20)

Рассмотрим разветвленную цепь проводов, в отдельных участках которой включены источники тока. Для такой цепи могут быть выведены два правила Кирхгофа. Сформулируем их.

1.     Это правило выражает закон сохранения заряда (5.4) для постоянного тока. Используем его в точках разветвления проводов (в узле).

               Þ               .

                        -                  (5.21)

Правило читается так:

Алгебраическая сумма всех токов, текущех к узлу и вытекающих из него, равна нулю.

Токи, текущие от узла, имеют знак “+”, токи, направленные к узлу, знак “‑”.

2. Выделим в цепи произвольный замкнутый контур. Применяя закон Ома (5.18) к каждому участку контура и суммируя, получим:

                      -                  (5.22)

Правило формулируется так:

Сумма падений напряжения на всех участках замкнутого контура равна сумме ЭДС, действующих в нем.

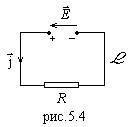Знак перед любым слагаемым второго правила Кирхгофа, являющегося следствием закона Ома, определяется следующим образом: перед  ставится “+”, если направление тока совпадает с направлением обхода контура;  записывается с “+”, если направление вектора сторонней напряженности  совпадает с направлением обхода контура L (рис.5.4.).