Испарение электронов с поверхности металлов называется термоэлектронной эмиссией.
Рассмотрим причины и условия этого явления. Электроны в металле и снаружи рассмотрим как два состояния электронного газа, находящегося в равновесии при определенных условиях. Потенциальная энергия электронов в металле меньше, чем снаружи. Зависимость потенциальной энергии электронов в металле ![]() от координаты
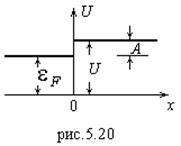
от координаты ![]() , начало которой отсчитывается от поверхности металла, представлена в виде графика на рис.5.20. Известно, что все уровни энергии до
, начало которой отсчитывается от поверхности металла, представлена в виде графика на рис.5.20. Известно, что все уровни энергии до ![]() (энергии Ферми) заняты. Следовательно, чтобы удалить из металла электроны, имеющие энергию, близкую
(энергии Ферми) заняты. Следовательно, чтобы удалить из металла электроны, имеющие энергию, близкую ![]() , необходимо затратить какую-то энергию
, необходимо затратить какую-то энергию ![]() , где
, где ![]() - работа выхода электрона из металла.
- работа выхода электрона из металла. ![]() ;
; ![]() , т.е.
, т.е. ![]() .
.
 Вне металла имеет место функция распределения:
Вне металла имеет место функция распределения:
![]() , (5.31)
, (5.31)
где ![]() - кинетическая энергия электрона. Это следует из (5.23) при
- кинетическая энергия электрона. Это следует из (5.23) при ![]() :
:
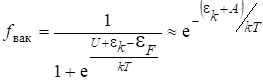 . (5.32)
. (5.32)
Так как ![]() и
и ![]() , то
, то ![]() . Из (5.31) видно, что вне металла осуществляется распределение электронов по энергиям не по статистике Ферми-Дирака, а по Больцману. Этого следовало ожидать, т.к. из металла могут вылетать лишь электроны в “хвосте”
. Из (5.31) видно, что вне металла осуществляется распределение электронов по энергиям не по статистике Ферми-Дирака, а по Больцману. Этого следовало ожидать, т.к. из металла могут вылетать лишь электроны в “хвосте” ![]() , где зависимость такая же, как в статистике Больцмана (см.рис.5.9).
, где зависимость такая же, как в статистике Больцмана (см.рис.5.9).
Нужно подсчитать число электронов ![]() , вылетающих из единицы объема металла при данной температуре в вакуум. Для этого необходимо знать число электронов по статистике Больцмана в интервале импульсов от
, вылетающих из единицы объема металла при данной температуре в вакуум. Для этого необходимо знать число электронов по статистике Больцмана в интервале импульсов от ![]() от
от ![]() и проинтегрировать от 0 до
и проинтегрировать от 0 до ![]() это значение. При этом
это значение. При этом ![]() изменяется непрерывно. В фазовом пространстве электроны, имеющие импульс, величина которого лежит в промежутке от
изменяется непрерывно. В фазовом пространстве электроны, имеющие импульс, величина которого лежит в промежутке от ![]() от
от ![]() , должны занимать объем в шаровом слое радиуса
, должны занимать объем в шаровом слое радиуса ![]() шириной
шириной ![]() :
: ![]() . Объем одной элементарной ячейки для электрона в
. Объем одной элементарной ячейки для электрона в ![]() - пространстве:
- пространстве: ![]() (следствие принципа неопределенностей). Тогда число электронов в интервале
(следствие принципа неопределенностей). Тогда число электронов в интервале ![]() с учетом функции распределения (5.31):
с учетом функции распределения (5.31):
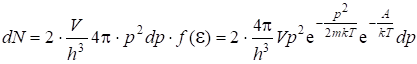 . (5.33)
. (5.33)
Тогда:
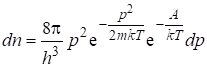 . (5.34)
. (5.34)
Как и ранее (§ 5.3), множитель “2” появляется вследствие учета того факта, что в каждой элементарной ячейке могут находиться два электрона с противоположной ориентацией спина. Из (5.34) следует, что:
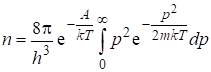 . (5.35)
. (5.35)
Сведем интеграл к интегралу Пуассона введением следующей замены: 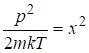 . Тогда
. Тогда ![]() . Принимая во внимание, что
. Принимая во внимание, что 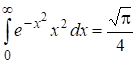 , получаем:
, получаем:
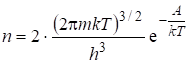 (5.36)
(5.36)
или
![]() ,
,
т.е. концентрация электронов, испарившихся с поверхности металла, растет с увеличением температуры.
Вычислим ток эмиссии: ![]() . Нужно учесть, что скорость также зависит от температуры:
. Нужно учесть, что скорость также зависит от температуры:
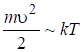 ;
; ![]() .
.
Тогда ток эмиссии:
![]() - (5.37)
- (5.37)
Это формула Ричардсона (1903 г.) – Дешмана (1923 г.). Оба отмечены Нобелевской премией в 1928 г. Влияние экспоненциальной зависимости от температуры иллюстрируют следующие величины тока для W:
для W: при 1000 К ![]() ;
;
при 2000 К ![]() ;
;
при 3000 К ![]() .
.
При малых температурах играет роль степенная зависимость, а при больших явно видна роль экспоненты. Нужно обратить влияние, что приведенные величины - это ток насыщения вакуумного диода, катод которого, сделанный из вольфрама, нагрет до соответствующей температуры.
Поможем написать любую работу на аналогичную тему

