Термоэлектрические явления - Основы статистической  физики - Лекции

Одним из важнейших применений линейной термодинамики необратимых процессов является построение теории термоэлектрических явлений. Экспериментально известны три термоэлектрических явления в изотропных средах.

Эффект Зеебека. На стыке двух различных проводников, имеющих разность температур , возникает ЭДС  (– коэффициент термо-ЭДС между данными проводниками, – коэффициент дифференциальной термо-ЭДС данного проводника). Поэтому из двух различных проводников составить замкнутую цепь и места их контактов поддерживать при различных температурах, то в этой цепи возникает ЭДС. Величина  считается положительной, если возникающий в проводнике ток течет от горячего контакта к холодному.

Эффект Пельтье. При прохождении электрического тока в термически однородной системе в месте соединения двух различных проводников выделяется или поглощается теплота (теплота Пельтье), пропорциональная силе тока.

Эффект Томпсона. При прохождении электрического тока в проводнике с градиентом температуры помимо джоулевой теплоты, выделяется добавочное количество теплоты (теплота Томпсона), пропорциональное градиенту температуры и силе тока.

Рассмотрим простейшую схему для реализации термоэлектрических явлений.

Будем считать, что электрическая цепь составлена из источника ЭДСΔU и двух разных проводников a и b, спаи которых помещены в термостаты 1 и 2 с температурами , . Явления переноса на обоих спаях и в области между термостатами, где , будем считать достаточно медленными, те перепад температур мал, сопротивление проводов достаточно велико, а ΔU достаточно мала.

Запишем общую формулу квазистатической термодинамики для этой системы:

.

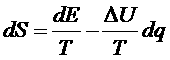Применим эту формулу для каждой из подсистем:

,

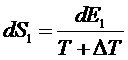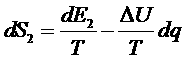
и запишем общее изменение энтропии:

.

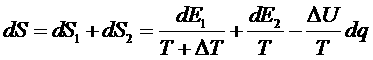Учитывая, что в изолированной в целом системе ,

получим с точностью до линейных членов:

.

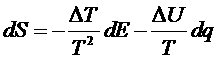Относя это изменение к единице времени, для скорости образования энтропии при заданных ΔT и ΔU получим

,

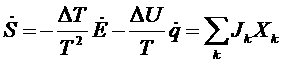где в качестве потоков можно выбрать электрический ток и поток энергии. Тогда выражения для потоков можно записать так:

,

.

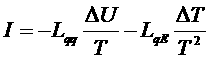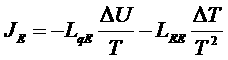Рассмотрим частные случаи и выясним физический смысл кинетических коэффициентов.

А) , .

Условие определяет величину термоЭДС, пропорциональную разности температур между спаями 1 и 2:

,

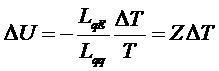причем коэффициент Z непосредственно измеряется, а если он известен, то полученное устройство (термопара) может служить прибором для измерения ΔTпо показанию вольтметра ΔU.

Измерение потока энергии

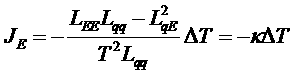
определяет коэффициент теплопроводности участка проводов между термостатами 1 и 2 при условии отсутствия тока. Поскольку материалы, из которых изготовлены провода, известны, то известны и табличные значения их коэффициентов теплопроводности.

Б), ΔT=0, эффект Пельтье

Выражение для тока

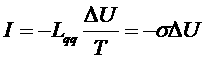
определяет проводимость σ в изотермической системе, а отношения потоков

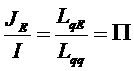
определяет так называемое тепло Пельтье, которое так же может быть измерено. Из четырех коэффициентов, характеризующих явления переноса А) и Б), независимыми должны быть только три. Мы уже фактически получили связь двух коэффициентов  - Зеебека и Пельтье:

.

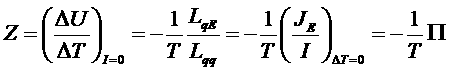Эта связь называется вторым соотношением Томсона. Заметим, что выделяемое на каком-либо спае тепло меняет знак при обращении тока, т.е. если , то

.

В) Эффект Томсона.

Спаи проводников в этом явлении роли не играют. Эффект возникает в однородном проводнике при наличии тока и градиента температуры. Мощность выделяющегося тепла можно записать в виде:

,

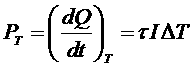где τ– постоянная величина.

Так как работа источника тока за секунду должна быть учтена в общем балансе энергии вместе с теплом Томсона на участках проводников с и теплом Пельтье на спаях, то согласно первому началу термодинамики с учетом правил знаков имеем (уточнить это правило!):

.

Разлагая в ряд величину

,

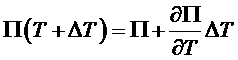и сокращая величину тока, приходим к так называемому «первому» соотношению Томсона:

.

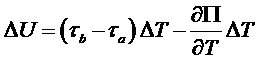Если подставить сюда соотношение для ΔU, то, сократив на ΔT, получим связь характеристик Томсона и Пельтье:

.

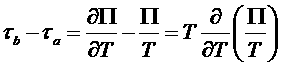Таким образом, характеристики пяти стационарных явлений переноса выражаются с помощью трех экспериментально измеряемых величин σ, æ и Π. Формальные коэффициенты Онсагера выражаются через них следующим образом:

, , .

Можно записать скорость производства энтропии, учитывая, что потоки можно записать в виде:

,

.

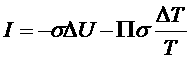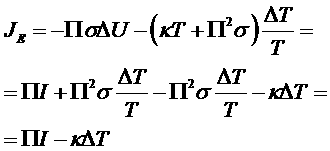Вводя вместо характеристики источника тока

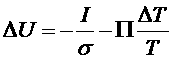
величину самого тока I, получим:

.

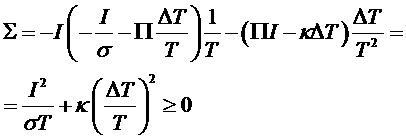Первое слагаемое связано с выделением джоулева тепла в секунду, а второе – с теплопроводностью.

С точки зрения статистической физики объяснение термоэлектрических явлений объясняется тем, что энергия электронов в каждом из металлов разная, поскольку уровень Ферми зависит от концентрации свободных электронов. В таком случае, при переходе из одного металла в другой электроны либо выделяют энергию (передают ее кристаллической решетке) либо поглощают.

Объяснение эффекта в первом приближении заключается в следующем. В условиях, когда вдоль проводника, по которому протекает ток, существует градиент температуры, причём направление тока соответствует движению электронов от горячего конца к холодному, при переходе из более горячего сечения в более холодное, электроны передают избыточную энергию окружающим атомам (выделяется теплота). При обратном направлении тока, проходя из более холодного участка в более горячий, электроны пополняют свою энергию за счёт окружающих атомов (теплота поглощается).

Для объяснения эффекта Томсона в металлах воспользуемся выражением для энергии электронов:

.

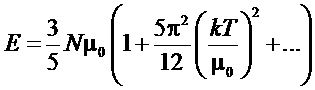В таком случае средняя энергия, приходящаяся на один электрон, будет иметь вид:

.

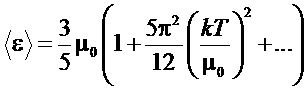Рассмотрим в проводнике объем V и найдем поток энергии в этот объем, обусловленный направленным движением электронов проводимости:

.

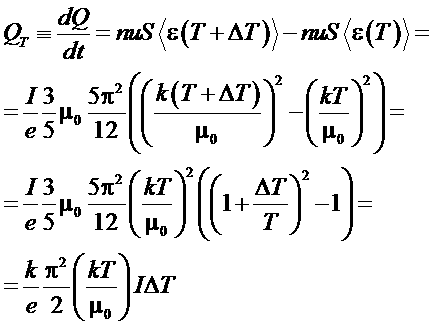Таким образом, видим, что коэффициент Томсона равен:

.

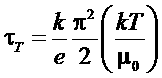Похожее выражение возникает и в других типах проводников (например, в полупроводниках).