Электромагнитные волны в вакууме.

Волновое уравнение.

Запишем уравнения Максвелла (7.11-7.15) для вакуума при :

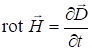; (7.24) ; (7.26)

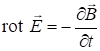; (7.25) . (7.27)

Материальные уравнения:

. (7.28)

Учтем, что:

. (7.29)

Оставим в уравнениях (7.24-7.27) лишь векторы и :

; ;

; .

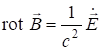Введя оператор “набла” , запишем последние четыре уравнения в виде:

; (7.30) ; (7.32)

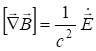(7.31) (7.33)

Задача состоит в нахождении решений этих дифференциальных уравнений, т.е. нахождении векторов поля и .

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимости Гарантии Отзывы

Применим векторно к (7.30) еще раз:

, (7.34)

так как , то:

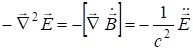. (7.35)

Используя известную из математики связь оператора Лапласа и оператора “набла”: , перепишем последнее уравнение в виде:

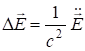. (7.36)

Аналогично можно получить:

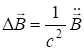. (7.37)

Уравнения (7.36), (7.37) называются волновыми. Ясно, что точно такие же уравнения можно записать для векторов и . Зная, что:

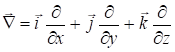, (7.38)

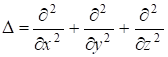, (7.39)

видим, что волновые уравнения являются дифференциальными уравнениями второго порядка.

Рассмотрим для простоты случай, когда и являются функциями лишь одной пространственной координаты, например, . Тогда (7.36):

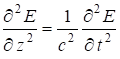. (7.40)

Плоская волна.

Решением уравнения (7.40) в общем виде является функция

. (7.41)

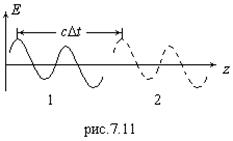Это волна, распространяющаяся вдоль оси в положительном или отрицательном направлении. Кривая на рис.7.11, описываемая функцией (7.41), из положения 1 спустя время передвинется целиком на и окажется в положении 2. Так как в любой произвольный момент времени значения постоянны в плоскости, перпендикулярной , такая волна называется плоской.

Докажем для общей функции , что она представляет собой волну. Для этого необходимо показать, что при :

, тогда .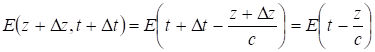

Итак, аргумент отвечает волне, движущейся вдоль оси . Точно так же можно доказать, что с аргументом записана волна, движущаяся против .

Самым простым решением волнового уравнения является монохроматическая плоская волна:

, (7.42)

где - фаза волны, ‑ волновой вектор (указывает направление распространения волны), ‑ радиус-вектор, проводится в точку, в которой производится наблюдение, - частота.

Волна называется монохрома-тической, если векторы и этой волны изменяются со временем по гармоническому закону с постоянной частотой.

Фазовая скорость – скорость движения поверхности постоянной фазы (см.рис.7.12)- отвечает условию:

=const

(на рис. - это плоскость, перпендикулярная оси , на которой значения постоянны, т.е. постоянна фаза волны). Тогда скорость движения этой плоскости вдоль может быть найдена так:

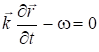Þ .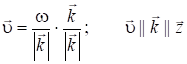

Запишем плоскую волну в комплексной форме:

(7.43)

Подставив (7.43) в уравнения Максвелла, можно получить:

; (7.30’)

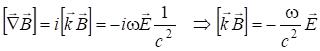; (7.31’)

. (7.33’).

. (7.32’).

Итак:

; (7.44) ; (7.46)

; (7.45) . (7.47)

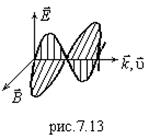Отсюда следует взаимная ориентация векторов (рис.7.13): ортогональны и образуют вместе с правую тройку векторов. Так как колеблются перпендикулярно , что было показано в общем виде уравнениями (7.46) и (7.47), то полученная электромагнитная волна поперечна. Видно также, что волны синфазны.

Из (7.44): , тогда:

Полученная плоская электромагнитная волна приведена на рис.7.13. Итак,

решением уравнений Максвелла в вакууме является плоская монохроматическая электромагнитная волна:

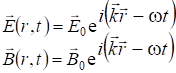. (7.48)

В электромагнитной волне векторы ортогональны и модули их связаны соотношением: .

Электромагнитная волна поперечна и векторы колеблются синфазно.

Определим вектор Умова-Пойнтинга:

, (7.49)

так как 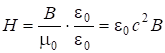. Из (7.49) следует, что вектор направлен так же, как и . Подставим в (7.49) значения (7.42):

Þ (7.50)

Видно из (7.50), что волна переносит энергию, т.е. она является бегущей. Скорость переноса энергии волны в вакууме равна фазовой скорости волны.

Фазовая скорость света в свободном пространстве.

Будем считать, что в свободном пространстве заряды и токи отсутствуют: r=0, j=0.

Материальные уравнения запишем в виде:

. (7.51)

Уравнение (7.44) изменится, если его записать для .

; ; . Тогда:

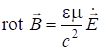. (7.52)

Тогда волновые уравнения запишутся в виде:

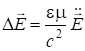
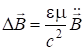. (7.53)

Решения волновых уравнений, по-прежнему, функции (7.48). Как и ранее, из условия =const находим - фазовую скорость.

Подставим решение (7.48) в волновое уравнение (7.53):

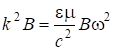. (7.54)

Отсюда находим фазовую скорость: 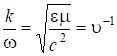и:

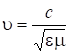. (7.55)

Обозначим - показатель преломления среды. Тогда фазовая скорость в свободном пространстве:

. (7.55’)

Для , , . Подставив векторы как функции времени и координат в (7.52), получаем связь между их модулями: .

Определим вектор Умова-Пойнтинга:

, .

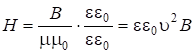Þ . (7.56)

Назовем величину среднего по периоду значения вектора интенсивностью. Тогда: - интенсивность электромагнитного излучения в свободном пространстве.

Сферическая волна.

Рассмотрим решение уравнений Максвелла в сферически симметричном случае. Все сводится к волновому уравнению в сферической системе координат (рис.7.14), для которой оператор Лапласа имеет вид:

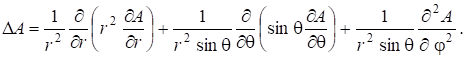(7.57)

Так как решение не зависит от угловых переменных (волна изотропна), то от (7.57) остается лишь первое слагаемое: .

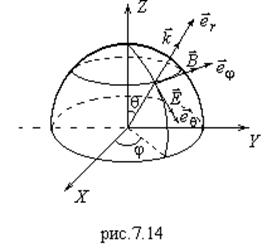
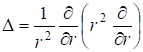. (7.57’)

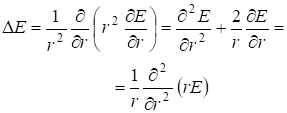Тогда (7.36) запишется в виде:

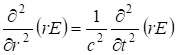. (7.58)

Решение уравнения (7.58) такое же, как и в предыдущем случае:

(7.59)

Так как и сонаправлены, то .

Данная волна называется сферической, поскольку поверхность, на которой в любой момент времени , является сферой.

Функция (7.59) от аргумента представляет расходящуюся от начала координат волну, а от аргумента - сходящуюся.

Для больших расстояний отдельные участки сферической поверхности можно рассматривать как плоскости. Если линейный размер участка велик по сравнению с длиной волны, волну можно считать плоской.

Стоячие волны.

Стоячая волна – это результат наложения двух бегущих волн одинаковой частоты и амплитуды, находящихся в противофазе:

(7.60)

. (7.61)

Из сравнения (7.60) и (7.61) видно, что и ‑волны, бегущие навстречу.

Рассмотрим структуру электромагнитного поля стоячей волны. Выберем ось вдоль направления распространения бегущей волны. Запишем компоненты и таким образом:

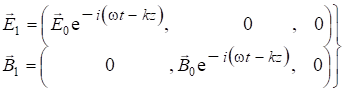. (7.62)

(7.62) - это волна, распространяющаяся вдоль оси .

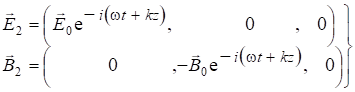. (7.63)

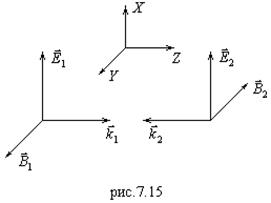(7.63) - это волна, распространяющаяся навстречу первой (рис.7.15). На рис. учтено, что векторы в каждой из волн образуют правую тройку векторов, при этом:

Найдем результирующее электромагнитное поле:

С использованием формул Эйлера получаем:

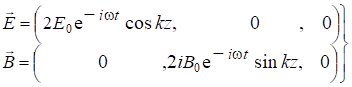(7.64)

или в вещественном виде:

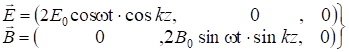. (7.65)

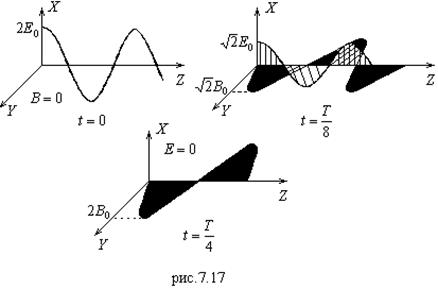
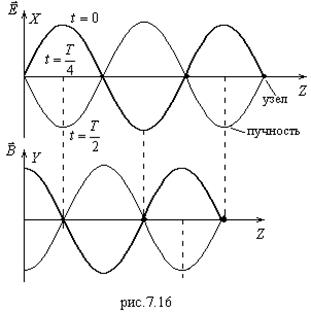Графически зависимость (7.65) представлена на рис.7.16. Видно, что амплитуды колебаний и изменяются в зависимости от Z от и до нуля. Вектор в каждой точке совершает колебания с частотой . В плоскости с координатой возникают пучности ( принимает значения от до -); в координате 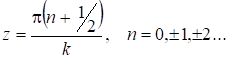образуются узлы и обращается в нуль. Колебания по разные стороны узла происходят в противофазе.