Считается, что если сила взаимодействия между двумя зарядами в вакууме: 
, то в среде сила взаимодействия будет в 
раз меньше:
. 
- диэлектрическая проницаемость, берётся из опыта. У разных веществ диэлектрическая проницаемость различная. Это чисто феноменологический подход, где константа определяется прямо из опыта.
В дальнейшем мы с вами будем рассматривать микроскопическую теорию, поскольку этот подход общий, удобный, практичный, но не всегда работает.
А микроскопическая теория позволяет на основе знания микроструктуры вещества и тех процессов, которые происходят в веществе, предсказать значение . Сейчас мы в это вдаваться не будем, но, по большому счёту, зависит и от температуры (для некоторых диэлектриков), и зависит от частоты, и ещё от целого ряда обстоятельств. Скажем сразу, что хоть 
и называется диэлектрической проницаемостью вакуума, но никакого отношения не имеет к диэлектрической проницаемости, оно необходимо для соблюдения размерности. Если переходить в Гауссовскую систему, как это сделано у И.Е. Тамма, то вообще не существует.
Тогда система уравнений для электрических полей в диэлектрики примет вид:
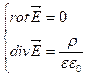
Если у нас однородный диэлектрик, то =const.
Введём 
- вектор электрической индукции:
.
Подставив данное уравнение в нашу систему, получаем
 |
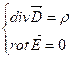
Рассмотрим поведение 
на границе раздела двух сред. В каждый из них разложим вектор напряжённости на нормальную и тангенсальную слагающую поверхности.
Воспользуемся уравнениями Максвелла для диэлектрика:
(по теореме Гаусса).
Вблизи раздела двух сред возьмём произвольную замкнутую поверхность с двух сторон так, чтобы граница раздела двух сред попадала в область S.
 |
S
Для простоты поверхность сожмём так, чтобы она плотно прилегала к этой поверхности раздела с одной и другой стороны.
Тогда интеграл распадётся на два интеграла: по поверхности 
и поверхности 
: 
- поверхностная плотность свободных зарядов. Для простоты предположим, что D вдоль поверхности не меняется. Эти интегралы примут вид:
Пусть n нормаль к поверхности границы раздела.
В этом случае 
- так как нормали совпадают по направлению.
- так как нормали противоположны по направлению.
Если нет поверхностных зарядов, то есть, если 
, то
Нормальное слагаемое испытывает скачок, то есть 
.
Если, например, 
, а 
, например, вода и воздух, стекло и воздух, то 
, то есть нормальное слагаемое вектора напряжённости при переходе из вакуума в среду c будет уменьшаться в 
раз.
А для тангенциальной слагающей воспользуемся витрорым уравнением для стационарным Эл. поля
Тогда из 
следует
,
,
S- поверхность ограниченная
контуром
Если ввести dt вдоль поверхности, то для тангенсальных составляющих вектора E, получаем
; 
Откуда следует, что тангенсальная составляющая скачка не испытывает.
 |
Силовая линия на границе двух сред испытывают преломление.
Поможем написать любую работу на аналогичную тему