Намагничивание.

Всякое вещество является магнетиком, то есть способно под действием магнитного поля приобретать внутренний магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле , которое накладывается на обусловленное токами поле . Оба поля в сумме дают результирующее поле в веществе: . Магнитные свойства вещества определяются магнитными свойствами электронов и атомов. По своим магнитным свойствам магнетики подразделяются на парамагнетики, диамагнетики и ферромагнетики. Мы рассмотрим диэлектрики первых двух классов. Для них в случае не сильных полей магнитная индукция равна , где  - магнитная проницаемость среды, а Н-напряжённость магнитного поля.

, где -магнитная восприимчивость, которая является коэффициентом пропорциональности между намагничиванием и полем . Задача нахождения  сводится к вычислению магнитной восприимчивости, а последнее вычисляется из формулы . Вычисление суммарного магнитного момента возможно при задании модели вещества. Известно, что магнетики разделяются на вещества, в которых в отсутствии магнитного поля нет магнитных моментов, в них магнитный момент индуцируется внешним полем в отличии поля в которых есть в молекулах магнитный момент в отсутствии магнитного поля. Вещества первого класса называются диамагнетиками, а второго парамагнетиками.

Задача сводится к вычислению магнитной проницаемости и магнитной восприимчивости. Последнее находится из . Вычисление сумм производится на основе учёта микроскопического модели вещества. Прежде всего рассмотрим общий эффект, который присутствует у всех магнетиков – диамагнитный эффект. В основе его лежит теорема Лармора, по которой под действием внешнего магнитного поля электроны начинают прецессировать вокруг него, создавая внутренние индукционные поля, направленные против внешнего поля. Рассмотрим детально это механизм прецессии.

Теорема Лармора.

Воспользуемся тем, что сила Лоренца во вращающей системе, связанной с электроном, будет проявлять себя как корриолисова сила . Откуда следует, что угловая частота вращения электрона, в прецессионном его движении, равна .

Пусть электрон движется в атоме со скоростью . Включаем внешнее магнитное поле. Орбита начнёт прецессировать вокруг магнитного поля с частотой , то есть электрон будет двигаться по сложной траектории. Тогда механический момент вращения будет равняться . А магнитный момент, связанный с этим механическим моментом будет равен . Скорость движения электрона складывается из двух скоростей: , -скорость электрона по орбите. Тогда магнитный момент будет равняться , где -собственный магнитный момент, а -прецессионный магнитный момент (дополнительный).

Пусть , тогда , где N-количество атомов в единице объёма. Будем считать, что в одном атоме только один электрон. , то

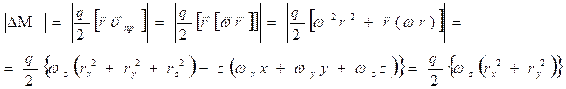
А так как: , то . 

Если число электронов равняется Z(число электронов или заряд ядра), то прецессионный магнитный момент для атома содержащих Z электронов будет равен , где z-атомарное число электронов в атоме. Если все они симметричны, то 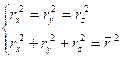  И следует, что:

,

.   Пусть  - средний квадратичный размера атома(обозначим, через а), то , а так как q<0, то -дополнительный магнитный момент. Намагничивае обусловлено прецессионным движением, тогда намагничивание вещества в каждой единице объёма содержащей одинаковое количество молекул, будет иметь вид:

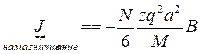 Магнитный момент направлен в противоположную сторону от дипольного момента.

Диамагнитов эффект-это эффект, при котором возникают индукционные токи, внутри которых создаётся поле, ослабляющее внешнее. Из последнего уравнения видно, что  - диамагнетика. Если у молекул вещества отсутствует собственные магнитные моменты и магнетизм обусловлен только эффектом прецессионного движения электронов, то такие вещества называются диамагнетиками, для них .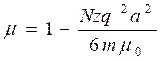

Парамагнетики. Парамагнетиками называются вещества, атомы которых в отсутствии внешнего магнитного поля имеют отличный от нуля магнитный момент. Существование этого магнитного момента может быть связанно как с движением электронов в атомах, так и со спиновыми магнитными моментами этих электронов. При внесении парамагнитного вещества в магнитное поле , в котором энергия каждого магнитного момента , эти магнитные моменты будут стремится повернуться по полю (чтобы их потенциальная энергия была минимальной) но их полная ориентация по полю невозможна, так как им противодействует тепловое движение молекул. Чисто формально, математический формализм этой задачи совпадает с математическим формализмом задачи поляризации дипольных моментов диэлектриков. Если мы теории поляризации заменим этих диэлектриков  , соответственно   и также разлагая функцию Ланжевена получим те же формулы полученные для диэлектриков. Формулы для магнитной восприимчивости запишется  и магнитная проницаемость будет равна . Для вещества, у которого уже имеются магнитные моменты атомов, третий член будет преобладать нд вторым, дисперсионным намагничиванием. Он имеет положительный знак и в отличии от диамагнитного эффекта, эффект ориентационный будет значительно больше себя проявлять. В нём заметен в частности тот же диамагнитный эффект

 Модуль вектора намагниченности в классической теории дипольных парамагнетиков выражается формулой , где -классическая функция Ланжевена от аргумента . Здесь  определяется по формуле . Парамагнетизм металлов обусловлен магнитными моментами электронами проводимости и магнитными моментами ионов кристаллической решётки. Эти электроны образуют сильно вырожденный газ, состояние которого мало меняется при изменении температуры. Таким образом,  направлен в ту же сторону, что и : . Поле усиливается.