Задача сводится к вычислению диэлектрической проницаемости на основе микроскопической модели вещества. И в конечном итоге сводится к вычислению дипольного момента в единице объема 
, где 
-дипольный момент отдельной молекулы. Для этого нужно задать микроскопическую модель вещества, которая для простоты будем предполагать находится в газообразном состоянии. Механизм поляризации будет различен для диэлектриков, у которых в отсутствии поля нет дипольного момента (в них под действием внешнего поля индуцируется дипольный момент) и диэлектрики, у которых изначально имеется магнитный момент. Рассмотрим диэлектрики для первого случая. Дипольный момент каждой отдельной молекулы равняется 
, 
- есть смещение электрона под действием внешнего поля. Оценим величину этого смещения.
Она определяется конкуренцией силы, разрывающей молекулы и силой, которая удерживает электрон вблизи молекулы. При малых полях имеет место закон Гука, где сила пропорциональна растяжению молекул (смещению электронов) 
. По закону Гука смещение электрона пропорционально внешней силе (напряжённости поля). 
, где 
-поляризуемость молекул, характерная для данного вещества. Тогда из , Поскольку растяжение диполей происходит в одном направлении вдоль поля, то дипольный момент в единице объёма 
, где 
-число молекул (диполей) в единице объёма, то вектор поляризации будет равный 
и 
. Обозначая 
получаем: 
, где 
-диэлектрическая проницаемость. Как мы видим она зависит для веществ с индуцированными диполями только от свойства вещества и концентрации (плотности).
Рассмотрим теперь поляризацию диэлектриков, молекулы которого, изначально имеют магнитны момент 
. В электрическом поле потенциальная энергия диполя во внешнем поле равна: 
.
Естественно диполи занимают такое расположение, при котором потенциальная энергия будет минимальна, то есть угол равняется нулю. Но это не происходит из-за столкновения молекул находящихся в тепловом движении. Пусть поле направленно вдоль оси z
В этом случае вектор поляризации будет складываться как геометрическая сумма дипольных моментов, то есть 
. Поделим и умножим на N. Получим:
, где величина 
, есть среднее значение для молекул в единице объёма. Получаем, что 
.
Как вычислить среднее значение для некоторой величины 
.
, где 
- число измерений при которых попалось значение 
.
, где 
- есть вероятность i-го события.
- среднее значение любой физической величины.
dwt – вероятность того, что физическая величина лежит в интервале от до 
. Аналогично: 
. Известна формула Больцмана для распределения молекул в поле тяготения: 
, где U=mgh.
Вероятность того, что частица будет наблюдаться в элементе объёма dV равна
константу можно найти положив 
, то
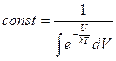
- элемент объема в сферической системе координат.
Соберём теперь всё вместе:
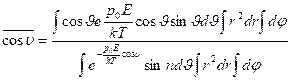
Введём обозначение 
В реальных полях 
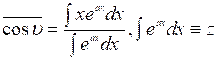
Легко видеть, что
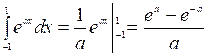
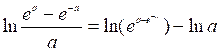
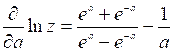
Тогда
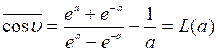- функция Ланджевена.
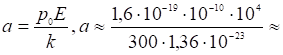
Если разложить в ряд 
Значит,
, где 
, где N – концентрация, Т, и Р вещества. 
зависит от Т, N(p)
Второй член в этом выражении обусловлен индукционной поляризацией вещества, присутствующей во всех веществах.
Поможем написать любую работу на аналогичную тему