Всякий реальный контур обладает активным сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают, Уравнение колебаний можно получить, исходя из того, что сумма падений напряжения на емкости, индуктивности и активном сопротивлении должна быть равна нулю:
L
Учтя, что 
равно квадрату собственной частоты контура 
о и введя обозначение
Последнее уравнение совпадает с дифференциальным уравнением затухающих механических колебаний.
Частота затухающих колебаний меньше собственной частоты o.
Разделив на емкость С, получим напряжение на конденсаторе:
U=
Чтобы найти силу тока, продифференцируем по времени:
Затухание колебаний принято характеризовать логарифмическим декрементом затухания
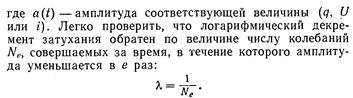
Колебательный контур часто характеризуют его добротностью Q, которая определяется как величина, обратно пропорциональная логарифмическому декременту затухания
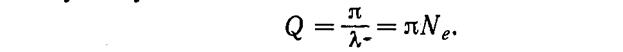
Добротность контура тем выше, чем большее число колебаний успевает совершиться прежде, чем амплитуда уменьшится в е раз.
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим. Значение критического сопротивления RK определяется условием 
. Откуда
Rk=2
Поможем написать любую работу на аналогичную тему