Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную э. д. с. или, разорвав контур, подать на образовавшиеся контакты переменное напряжение U. Приравняем сумму падений напряжения на элементах контура приложенному напряжению
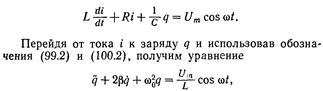
Разделив заряд q на емкость С, получим напряжение на конденсаторе
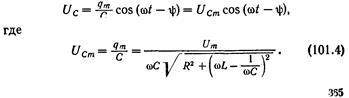
Продифференцировав функцию по t, найдем установившийся ток в контуре
Амплитуда тока имеет значение
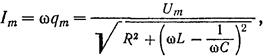
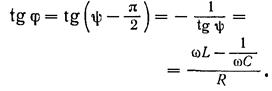
Резонансная частота для заряда q и напряжения на конденсаторе Uc равна
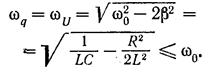
Резонансные кривые для Uc изображены на рис. 219 (резонансные кривые для q имеют точно такой вид). Они сходны с резонансными кривыми, получающимися для механических колебаний (см. т. I, рис. 189). При 
—>0 резонансные кривые стремятся к UCm=Um— напряжению, возникающему на конденсаторе при подключении его к источнику постоянного напряжения величины Um. Максимум при резонансе получается тем выше и острее, чем меньше 
, т. е. чем меньше активное сопротивление и больше индуктивность контура.
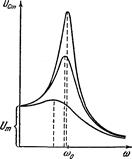
Резонансные кривые для силы тока изображены на рис. 220. Они соответствуют резонансным кривым для скорости при механических колебаниях. Амплитуда силы тока (101.6) имеет максимальное значение при 
= 0. Следовательно, резонансная частота для силы тока совпадает с собственной частотой контура 
Отрезок, отсекаемый резонансными кривыми на оси Im равен нулю — при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.
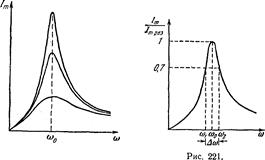
где Q — добротность контура.
Добротность контура характеризует также остроту резонансных кривых.
Поможем написать любую работу на аналогичную тему