При перемещении заряда в электростатическом поле, действующие на заряд кулоновские силы, совершают работу. Пусть заряд q0>0 перемещается в поле заряда q>0 из точки С в точку В вдоль произвольной траектории (рис.1.12). На q0 действует кулоновская сила
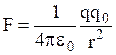. При элементарном перемещении заряда dl, эта сила совершает работу dA
, где a - угол между векторами 
и 
. Величина dlcosa=dr является проекцией вектора на направление силы 
. Таким образом, dA=Fdr, 
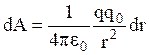. Полная работа по перемещению заряда из точки С в В определяется интегралом 
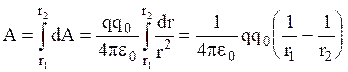, где r1 и r2 - расстояния заряда q до точек С и В. Из полученной формулы следует, что работа, совершаемая при перемещении электрического заряда q0 в поле точечного заряда q, не зависит от формы траектории перемещения, а зависит только от начальной и конечной точки перемещения.
В разделе динамики показано, что поле, удовлетворяющее этому условию, является потенциальным. Следовательно, электростатическое поле точечного заряда - потенциальное, а действующие в нем силы - консервативные.
Если заряды q и q0 одного знака, то работа сил отталкивания будет положительной при их удалении и отрицательной при их сближении (в последнем случае работу совершают внешние силы). Если заряды q и q0 разноименные, то работа сил притяжения будет положительной при их сближении и отрицательной при удалении друг от друга (последнем случае работу также совершают внешние силы).
Пусть электростатическое поле, в котором перемещается заряд q0, создано системой зарядов q1, q2,...,qn. Следовательно, на q0 действуют независимые силы 
,
равнодействующая которых равна их векторной сумме. Работа А равнодействующей силы равна алгебраической сумме работ составляющих сил, 
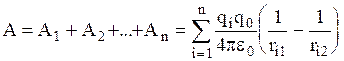, где ri1 и ri2 - начальное и конечное расстояния между зарядами qi и q0
.
Поможем написать любую работу на аналогичную тему