Элементарная классическая теория электропроводности металлов

Носителями тока в металлах являются свободные электроны, т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде (1863—1906) и разработанной впоследствии нидерландским физиком X. Лоренцем.

По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость теплового движения электронов

которая для Т=300 К равна 1,1 · 105 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.

Вывод основных законов электрического тока в классической теории электропроводности металлов.

1. Закон Ома. Пусть в металлическом проводнике существует электрическое поле напряженностью Е=const. Co стороны поля заряд е испытывает действие силы  приобретает ускорение . Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость

где <t> — среднее время между двумя последовательными соударениями электрона с ионами решетки.

Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона

.                  

Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время <t> свободного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относительно кристаллической решетки проводника, равной  ( — средняя скорость теплового движения электронов). В § 102 было показано, что , поэтому

Подставив значение (t) в формулу (103.1), получим

.

Плотность тока в металлическом проводнике, по (96.1),

,

откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получили закон Ома в дифференциальной форме. Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость материала

,                                                         

которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.

2. Закон Джоуля — Ленца. К концу свободного пробега электрон под действием: поля приобретает дополнительную кинетическую энергию

.                             

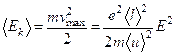При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание.

За единицу времени электрон испытывает с узлами решетки в среднем <z> столкновений:

.                                                     

Если n — концентрация электронов, то в единицу времени происходит  столкновений и решетке передается энергия

,                                                   

которая идет на нагревание проводника. Подставив (103.3) и (103.4) в (103.5), получим таким образом энергию, передаваемую решетке в единице объема проводника зш. единицу времени,

.                                                 

Величина w является удельной тепловой мощностью тока. Коэффициент пропорциональности между w и Е2 по (103.2) есть удельная проводимость ; следовательно, выражение (103.6) — закон Джоуля — Ленца в дифференциальной форме.