Трудности классической теории электропроводности.

Явление сверхпроводимости.

   Свойства вещества в сверхпроводном состоянии:

1)                       Ток, однажды возникнув в таком проводнике, будет протекать годами

2)                       Отсутствует магнитное поле внутри проводника

3)                       Внешнее магнитное поле не проникает в сверхпроводник

4)                       Очень сильный ток или очень сильное внешнее магнитное поле могут разрушить состояние сверхпроводимости.

1) Температурная зависимость проводников. Согласно экспер. данным сопр. металлов увелич. с температурой по з-ну R=R0+aT, где R0-сопр. при T=273K, a=1/273 град-1. Для r ф-ла аналогична r=r0+aT. Согл. опыта r~T. r=2máVTñ/(ne2álñ)Þr~áVTñ. На осн. КЭТ след. r=ÖT, т.е. теория расходится с опытом.

2) Теплоёмкость металлов и диэлектриков. Согл. опвтов атомная теплоёмк. металлов и диэл-ков одинакова (C=3R, где R-газовая постоянная). Это положение наз. з-н Дюлонга и Пти. Согл. КЭТ металл сост. из кристал. решётки и своб. эл-нов, а диэлектрик своб. эл-нов не имеет. Следует ожидать, что теплоёмк. металлов=т.ё. кристал. решётки+т.ё. своб. эл-нов (Cмет=R+3/2R=4,5R), чего нет на опыте.

Электронный газ, на самом деле подчиняется не классической статистике Максвелла, а квантовой статистике. Затруднения устраняются в квантовой теории проводимости. Несмотря на затруднения, КЭТ она проста и широко применяется при высоких темп-рах и малых концентрациях.

Температурная зависимость сопротивления. Из формулы удельной проводимости 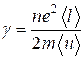 следует, что сопротивление металлов, т. е. величина, обратно пропорциональная , должна возрастать пропорционально . Этот вывод электронной теории противоречит опытным данным, согласно которым .

Оценка средней длины свободного пробега электронов в металлах. Чтобы по формуле  получить , совпдающие с опытными значениями, надо принимать <l> значительно больше истинных, иными словами, предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний, что не согласуется с теорией Друде — Лоренца.

Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Согласно закону Дюлонга и Пти, теплоемкость одноатомного кристалла равна 3R. Учтем, что теплоемкость одноатомного электронного газа равна . Тогда атомная теплоемкость металлов должна быть близка к 4,5R. Однако опыт доказывает, что она равна 3R, т, е. для металлов, так же как и для диэлектриков, хорошо выполняется закон Дюлонга и Пти. Следовательно, наличие электронов проводимости практически не сказывается на значении теплоемкости, что не объясняется классической электронной теорией.

Указанные расхождения теории с опытом можно объяснить тем, что движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой.

16 Формула Ричардсона-Дэшмена. Работа выхода электронов из металла.

Ток насыщения определяется формулой Ричардсона - Дешмана:

A – работа выхода электрона из катода, T – термодинамическая температура, С - постоянная

РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА.

Работа, которую необходимо совершить для удаления электрона из металла в вакуум называется работой выхода. Причин появления работы выхода две. В месте, которое покинул электрон возникает избыточный положительный заряд и электрон притягивается к нему. Второе: над поверхностью металла создается электронное облако на расстоянии порядка размеров атома. Оно образует с наружным слоем положительных ионов двойной электрический слой, поле которого, подобно полю конденсатора. Толщина этого слоя равна нескольким межатомным расстоянием. Этот слой не создает электрического поля во внешнем пространстве, но препятствует выходу электронов из металла. При вылете из металла электрон должен преодалеть эл. поле. задерж. поля. Т.к. при вылете электрона из металла потенциал металла возрастает, на границе металл-вакуум появляется скачок потенциала, называемый поверхностным скачком потенциала, которым и определяется работа выхода электронов из металла. ∆φ=A/e; Т.к. поле вне двойного жлектрического поля отсутствует, то потенциал вакуума равен нулю, а потенциал металла “+” и равно ∆φ. Электрон в металле имеет “-” – значение энергии и его можно рассматривать как частицу, находящуюся в потенциальной яме. Глубина этой ямы равна работе выхода. В различных материалах изменяется от 4 до 25 ЭВ и зависит от химической природы металла и чистоты его поверхности.