При наблюдении в телескоп на объектив падает параллельный пучок лучей и в связи с ограниченностью отверстия в фокальной плоскости объектива возникает дифракционная картина. В отверстие объектива помещаются небольшое число зон Френеля, так как площадь зон зависит от расстояния до объекта 
. В связи с чем, при наблюдении двух очень близких звезд, даваемые ими дифракционные картины частично перекрываются и наблюдается неоднородное по освещенности светлое пятно.
Будем придерживаться критерия Релея, который требует для разрешения изображений, чтобы максимум одной кривой дифракции приходился на минимум второй кривой. Условие минимума в данном случае имеет значение
, (31)
где D – диаметр объектива. Радиус темного кольца на экране (минимум) в фокальной плоскости объектива будет 
или, подставляя (31) получим разрешенное расстояние 
, (32)
видно, что с увеличением D разрешенное расстояние уменьшается, т.е. можно увидеть более близкие друг к другу звезды.
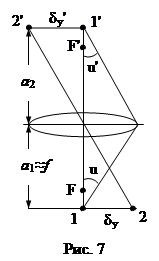
У микроскопа предмет находится вблизи объектива, поэтому будем рассматривать две соседние точки и от них лучи можно считать параллельными и рассматривать дифракцию этих лучей как Фраунгоферову. Обозначим через dу расстояние между едва разрешенными точками объекта. Принимая условие синусов Аббе 
, где n и n¢ коэффициенты преломления вещества перед объективом и после него, u и u¢ углы раскрытия (рис 7). Из условия разрешенного расстояния имеем
(33)
Из рисунка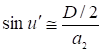 
, тогда
(34)
из (33) и (34) получим
(35)
и 
(36)
А= nsinu – называется числовой апертурой объектива. Если объектив находится в воздухе (n=1), а угол u для микроскопических объектов близких к 
, то разрешенные точки на объекте могут находиться на расстоянии 
друг от друга.
Поможем написать любую работу на аналогичную тему