Рассмотрим малое тело, движущееся в инерциальной системе отсчета k со скоростью u. Пространственно-временные координаты этого тела (t, r). Перейдем в другую инерциальную систему отсчета k’
, начало координат которой движется относительно начала координат системы k со скоростью b. Найдем скорость u’ этого тела в системе k’.
Запишем преобразования (F10) для дифференциалов координат:
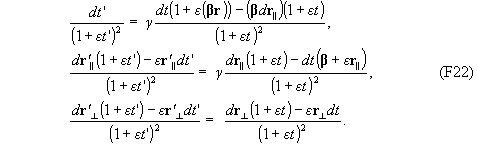
Введем вспомогательные величины r 0 = r -ut и r’0 = r’ -u’t’. Разделим почленно второе и третье равенство (F22) на первое:
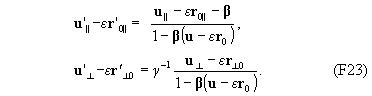
Полученные выражения связывают скорость тела, измеренную в системе k в пространственно-временной точке (t , r), со скоростью, измеренной в системе k’ в той же мировой точке с координатами (t’, r’).
Полученные выражени удобны для анализа свойств преобразований Лоренца-Фока, но неудобны дл практических расчетов, так как левые части равенств (F23) содержат скорость в неявном виде (через r’0).
Выразим координаты r’0 через r0 . Для этого запишем преобразования (F10) , подставив в левую часть координаты (t’=0,
r’=r’0):
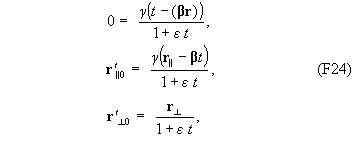
С учетом первого равенства (F24) и определени r0 =r-ut, получаем
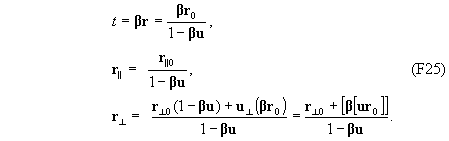
Подставляя полученные выражения в правые части (F24), имеем
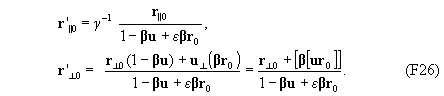
Теперь можно переписать равенства (F23)

Несмотря на громоздкость, полученные соотношени удобны для непосредственных вычислений - подставляя в правые части равенств (F27) значения скорости тела в некоторой мировой точке (t, r) мы получаем скорость тела в произвольной инерциальной системе отсчета в той же мировой точке.
Поможем написать любую работу на аналогичную тему

