Вернемся кзакону сложения скоростей в форме (F23)
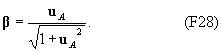
Если в системе отсчета k тела (галактики) движутся со скоростями, пропорциональными расстоянию до начала координат u = er0, то в системе k’ имеет место соотношение u’ = e r’0- b. Из формулы (F26) следует, что
r’^0= r^0, r’||0= g-1r||0. Для восстановления ковариантности картины разбегания галактик необходимо:
1) уменьшить пространственные масштабы в системе k ’ вдоль направления b в g раз:
u’ Þg -1 u’, r’||0 Þ g-1 r’||0
(после этого r’||0 = r|| 0 и u’
= er’0-g b),
2) перенести начало пространственных координат в другую галактику r’0Þr’0+ eg b.
Окончательно получаем ковариантность равенства u =
er0, связывающего скорости и координаты точек «хаббловской» вселенной. Подобная процедура для обычных преобразований Лоренца не приводит к ковариантной картине, так как знаменатели в выражениях (F26) не обращаются в единицу.
Заметим, что построенное преобразование координат переводит начало отсчета в некоторую точку A, двигавшуюся в системе k со скоростью u A = r A0 = g b, или
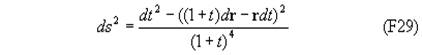
Построенное преобразование с параметром b обладает одной важной особенностью — переход в систему отсчета k’ возможен при любых значениях скорости uA (и, следовательно, расстояния r A0), так как | b|
Заметим, что при |uA|k сделать трансляцию — перенос начала отсчета на расстояние r A0 = uA, затем выполнить преобразование Лоренца-Фока с параметром b= uA. Однако, при |uA|>1 перестановка операций невозможна.
Итак, картина расширения Вселенной с постоянной Хаббла, равной e, выглядит одинаково для наблюдателей, находящихс в любой галактике. В обычной системе единиц для постоянной Хаббла получаем H0= c/R . Используя экспериментальное значение
![]()
можно определить параметр преобразования Лоренца-Фока
![]()
Поможем написать любую работу на аналогичную тему

