Найдем геометрическое место точек пространства Минковского, связанных преобразованиями Лоренца-Фока (F9).
Соотношения (F10) позволяют найти инвариант преобразований (F9):
![]() .
.
Так желегко из (F10) находится дифференциальный инвариант
![]()
Положим для определенности e =1 и построим аналог времени- и пространственно-подобных гиперболоидов. Для положительных значений инварианта (F13) имеем
![]()
Здесь t -
«собственное время» - время в системе отсчета, в которой r=0.
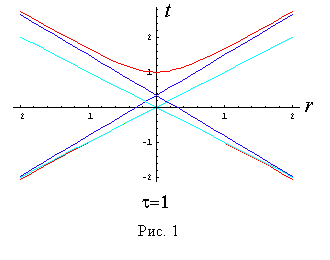
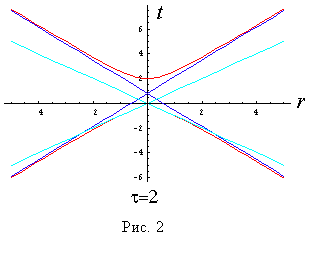
На рис. 1 представлен «гиперболоид» на плоскости t, r, соответствующий t =1, на рис. 2 - соответствующий t=2.
Прямыми линиями показаны световой конус и асимптотики «гиперболоида» на бесконечности:
![]()
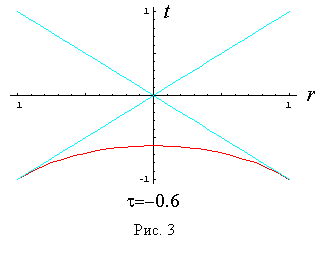
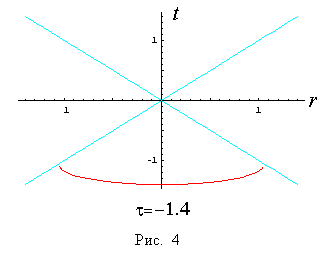
Отрицательным значениям t = - 0.6 и t - 1.4 соответствуют «гиперболоиды» на рис. 3 и рис. 4.
Для отрицательных значений инварианта (F13) имеем
![]()
Здесь l - расстояние от точки до начала координат в системе отсчета, в которой t=0.
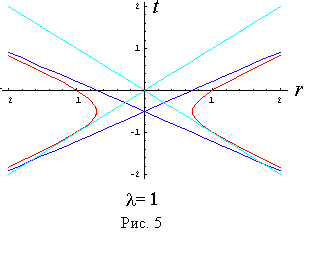
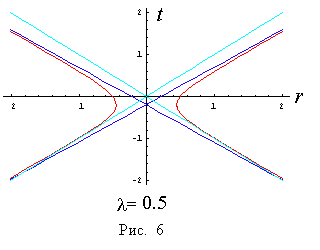
Значениям l=1 и l= 0.5 соответствуют однополостные «гиперболоиды» на рис. 5 и рис. 6.
Здесь асимптотические значения
![]()
Поможем написать любую работу на аналогичную тему

