Фотоны, брадионы, тахионы

Из равенств (F14)-(F35) следует, что допустимые для «брадионов» (частиц, движущихся про времениподобным мировым линиям, или, иначе, частиц с m2>0) значения скорости и расстояния удовлетворяют соотношению
|v-r0| < 1 (или в обычной системе единиц |v — H 0r0| < c).
Для «тахионов» (m2<0) получаем |v - r0| > 1, а для «фотонов» (m2 = 0) допустимы только движения вдоль световых конусов |v - r0| = 1. 
Рассмотрим подробнее геометрию световых конусов. Перепишем инвариант (F29) в обычной системе единиц

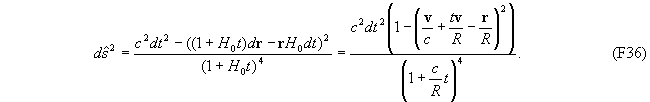
Это выражение инвариантно относительно преобразований (F8), в которых начала координат систем отсчета совпадают при t = t’ = 0. Заметим, что особой инвариантной точкой преобразований (F8) вляется момент t = t’ = R/c. Будем отсчитывать время от этой точки, т. е. произведем сдвиг начала отсчета времени на величину R/c:

t => t — R/c, t’ => t’ — R/c.

Теперь начала координат систем отсчета совпадают в момент t = t’ = R/c = t0 . Cкорость движения системы отсчета k’ в системе k обозначим u = -r0/t0. Величина r 0 = -ut0 определяет положение начала отсчета системы k’ в системе k в момент времени t = 0. 
Преобразования (F8) принимают вид

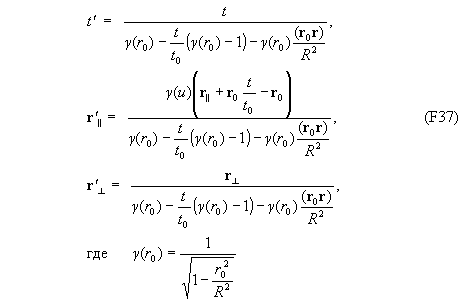
а инвариант (F36):

Четырехвектор (F31) можно переписать в виде

а четырехвектор энергии импульса (F33) частицы с массой m 

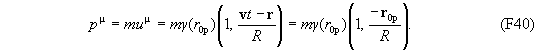
 В формулах (F38)-(F40) введена величина r0p = r-vt , имеющая смысл координаты частицы (точки) в момент t=0.
Примем, что выражения, входящие в (F40), являются энергией

и импульсом

частицы с массой m.
При t = 0 все частицы находятся внутри сферы r2=R2 и их распределение в пространстве определяется отношением массы (или импульса) к энергии по закону

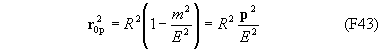
Скорости частиц в этот момент времени произвольны и не связаны с энергией.
Теперь рассмотрим геометрию движения фотонов.
Из вида инварианта (F38) или выражения для g(r0p)

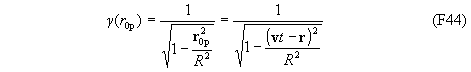
следует, что световые конуса ds 2=0 или, иначе, траектории частиц с нулевой массой, проходят через точки r0p2 = R2 в начальный момент времени. Скорости фотонов в этой точке могут принимать любые значения. Вылетая из начальной точки с некоторой скоростью c, фотон движется по траектории

Скорость фотонов, попадающих в момент времени t в точку с координатой r, равна

Фотоны, попадающие в начало координат (точку r = 0) в некоторый момент времени t, имеют скорость

Световой конус для некоторой точки t1, r1 задается соотношением

Зависимость скорости света от времени и положения в пространстве не противоречит постоянству константы c, потребованному при выводе преобразований Лоренца-Фока (F37). Действительно, эти преобразования написаны для систем координат, начала которых совпадают в момент времени t0=R/c.
Константа этих преобразований равна скорости света в момент времени t0 в начале координат.
Для преобразований в другой момент времени изменится велиичина t 0. Формально инвариант (F38) и вектор (F39) зависят от t0 , однако вектор (F40) и все последующие рассуждения инвариантны относительно выбора момента преобразования координат. Величина

инвариантна относительно преобразований Лоренца-Фока (F37) с любым значением параметров t0 и r0. Во избежание недоразумений отметим, что параметр r0 определяет скорость движения системы отсчета k’ относительно системы k: u = -r0/t0, а параметр r0p определяет скорость движения точки (частицы) в системе k: v = (r-r0p)/t.
Те величины, которые обычно называют энергией и импульсом частицы, отличаются от введенных выше (формулы (F41) и (F42)) размерным множителем — скоростью света в данный момент времени:

Видим, что эти величины для свободной частицы не сохраняются. Настоящими импульсом и энергией следует считать E и p, определяемые по формулам (F41) и (F42).
Отметим интересное свойство преобразований Лоренца-Фока. Если в выражении (F37) перейти к пределу t0=> 0, учтя при этом, что r 0 = -ut0, а 1-g (r0) => (ut0)2 /(2R2), получим преобразования Галилея

Этого и следовало ожидать, так как при t0= 0 скорость света бесконечно велика.