Перепишем преобразования (F1) в трехмерных векторах и учтем изотропность пространства:
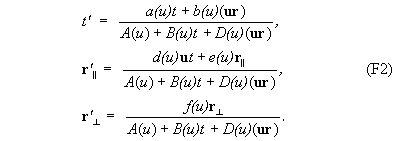
Определим вид этих функций.
1. Замена r||на - r||, r’|| на - r’||, u на - u не должна менять вид преобразования (F2), так как такая замена достигается простым поворотом на угол p вокруг направления r^. Следствие: все неизвестные функции в формулах (F2) должны быть или одновременно четными, или одновременно нечетными. Для определенности выберем вариант четных функций, т. е.
a(-u)= a(u), b(-u)= b(u),
d(-u)= d(u), e(-u)= e(u), f(-u)= f(u),
A(-u)= A(u),
B(-u)= B(u),
D (-u)=
D(u)
2. Точка r’=0 движется в системе отсчета k со скоростью u:
d(u)= - e(u)
3. Точка r =0 движется в системе отсчета k’ со скоростью -u:
a(u)= - d(u) = e(u)
Заменим b(u)= -a(u)g(u) и получим
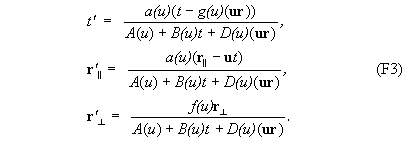
4. Обратное преобразование из k’ в k должно получаться из прямого (F3) заменой u на -u:
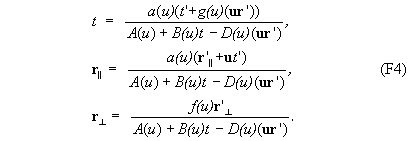
Комбинация прямого (F3) и обратного (F4) преобразований приводит к тождеству, откуда следует
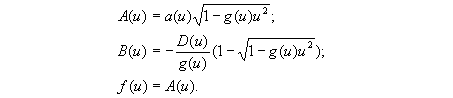
Произведя замену
D(u)=h(u)A (u)
и
![]()
получаем
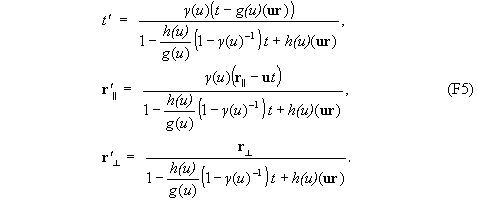
5. Произведем преобразование из системы k’ в систему k’’, движущуюся относительно k’ со скоростью u’||u. (Условие параллельности скоростей u и u’ облегчает вывод, но не является принципиальным).
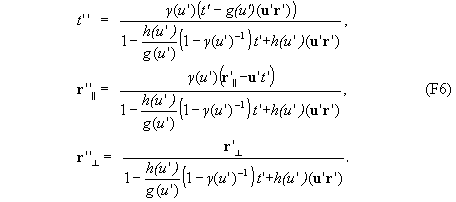
Комбинируя преобразования (F5) и (F6), получаем преобразование из k в k’’ с некоторой относительной скоростью u’’. Такое преобразование
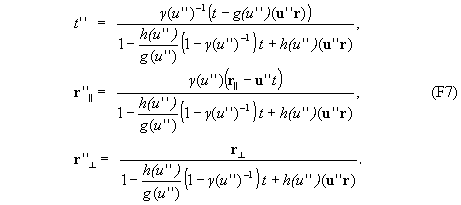
получится при подстановке выражений (F5) в правую часть равенств (F6), если
![]()
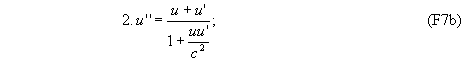
![]()
где c - постоянная величина размерности скорости, R - постоянная величина размерности длины (знак этой величины не определен).
Окончательный вид преобразований (F5)
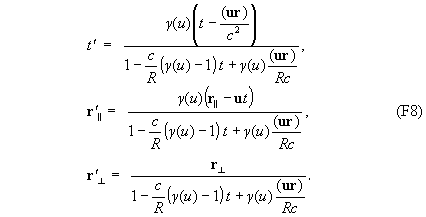
При r<<|R| и ct<<|R| преобразовани (F8) совпадают с обычными преобразованиями Лоренца.
Перейдем к системе единиц, в которой c=1, |R |=1. В этой системе скорости измеряютс в единицах c, а расстояния и время - в единицах |R|. Пусть e=sign. Преобразования (F8) принимают вид
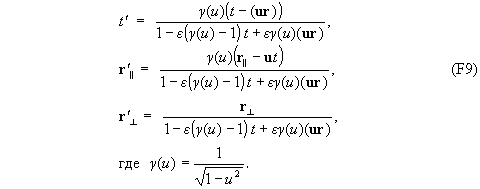
Легко убедиться, что формулы (F9) эквивалентны следующим преобразованиям
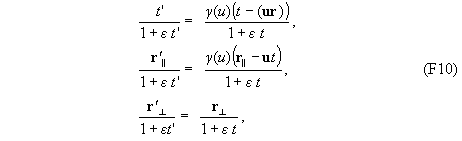
т. е. обычным преобразованиям Лоренца для величин
![]()
Заметим, что обратное к (F11) преобразование отличается от прямого знаком e :
![]()
Поможем написать любую работу на аналогичную тему

