Общие принципы расчета брутто-, нетто-ставки и нагрузки

Расчеты брутто- и нетто-ставки ориентируются прежде всего на расчет нетто-ставки, представляющую собой один из основных показателей финансовой устойчивости и платежеспособности страховщика:

∑СВ(П) = ∑СВып                                    (1)

где ∑СВ(П) — страховые взносы (премии) страхователей;

∑СВып - страховые выплаты страховщиков.

Рассчитав правую часть равенства (1), получают необходимую величину левой части.

Методика расчета нетто-ставки по конкретному виду или однородным объектам страхования сводится к определению среднего показателя убыточности страховой суммы за определенный период, затем оценивается его устойчивость. На основе полученных данных решается вопрос о необходимости расчета и величине рисковой надбавки (дельта-надбавки).

Показатель убыточности страховой суммы математически выражает вероятность ущерба в виде доли совокупной страховой суммы, которая выбывает из страхового резерва (фонда) в связи с наступлением страховых случаев и соответствующих выплат. Эта доля (единица страховой суммы или объекта страхования либо процентная ставка от совокупной страховой суммы) и составляет основу расчета нетто-ставки. Убыточность страховой суммы — величина синтетическая и зависит от различных факторов. Их можно свести к трем показателям, которые называют элементами убыточности:

1.  - частость (частота) страховых случаев: отношение количества страховых случаев к числу застрахованных объектов;

2.  — опустошительность одного страхового случая: отношение числа пострадавших объектов к числу страховых случаев (показывает среднее число объектов, пострадавших от одного страхового случая);

3. -— отношение рисков: отношение средней страховой выплаты по одному пострадавшему объекту (к) к средней страховой сумме одного застрахованного (i).

Расчетным показателем страховой статистики служит частота (частость) страховых событий — соотношение между числами страховых случаев и застрахованных объектов. Зная вероятностное число страховых случаев за определенный период, можно определить и степень вероятности их наступления. Она представляет собой отношение количества страховых случаев к числу застрахованных объектов.

Математически это выражается вероятностью наступления, предположим, события К при отношении числа неблагоприятных случаев М к общему числу равновозможных — N теории вероятностей отношение числа элементарных исходов, не благоприятствующих событию К, к их общему числу называют вероятностью события К и обозначают

                                (2)

Поскольку вероятность всегда выражается правильной дробью (числитель меньше знаменателя), то вероятность Р события К всегда будет соответствовать выражению 0≤Р(К)≥1. Если вероятность события достигает крайних значений (0 или 1), то страхование на случай наступления данного события проводиться не может. Страховые отношения складываются только тогда, когда заранее неизвестно, произойдет за данный период времени страховой случай поданному страховому событию или нет.

Отношение числа испытаний, в которых событие К появилось М раз, к общему числу фактически произведенных испытаний N называют относительной частотой F события К, или статистическим весом:

                                (3)

Первое определение вероятности называют классическим (вероятность наступления события до опытов), второе - статистическим (относительная частота появления события в результате проведения опытов).

Исходным данным для расчета нетто- и брутто-ставок является вероятность ущерба, лежащая в основе нетто-ставки, которая зависит, в свою очередь, от вероятности наступления страхового случая:

                                   (4)

где Ру, — вероятность ущерба;

Рсс - вероятность наступления страхового случая.

Зная число страховых случаев за тарифный период, можно определить и степень вероятности их наступления. Она представляет собой отношение числа страховых случаев к количеству застрахованных объектов:

                                 (5)

где Чсс - число страховых случаев;

Кэо - количество застрахованных объектов.

При расчете нетто- и брутто-ставок предполагается, что массовых страховых случаев не будет (например, гибели самолета, теплохода с людьми и т. п.). Расчет тарифов проводится по заранее известному (или планируемому) количеству застрахованных объектов или договоров. При наличии перечисленных условий расчет средней убыточности страховой суммы производится по формулам (6)-(8):

                               (6)

где   - вероятность наступления страховых случаев;

Ру — вероятность ущерба;

 - коэффициент тяжести ущерба.

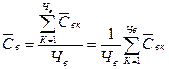                       (7)

где  - средняя страховая выплата по числу застрахованных объектов или договоров

 - средняя выплата при К-м страховом случае (К=1, 2, …Чв)

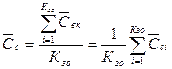                             (8)

где  - средняя страховая сумма по числу застрахованных объектов (Кзо)

 - страховая сумма по одному застрахованному объекту (i=1, 2, …Кзо)

Для введения рисковой надбавки и расчета ее величины после определения среднего показателя убыточности страховой суммы за тарифный период строится динамичный ряд показателей убыточности страховой суммы и оценивается его устойчивость.

Пример: Предположим, в среднем по туристской фирме сложились следующие показатели убыточности страховой суммы по добровольному страхованию личного имущества (багажа) туристов со 100 руб. страховой суммы (табл. 1).

Таблица 1.

Средняя за 5 лет величина убыточности страховой суммы (Усс) составит 15,8 ((17+16+16+15+15) / 5).

Оценка устойчивости динамического ряда производится с помощью математико-статистических коэффициентов вариации и медианы.

Для определения коэффициента вариации как отношении среднего квадратического отклонения к средней арифметической динамического ряда произведем расчет величины первого (σ) по приведенным данным второго. Для тарифных расчетов применяется следующая формула среднего квадратического отклонения:

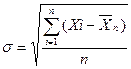                              (9)

где Хi — отклонения вариантов (показателей);

 — среднее арифметическое показателей;

п - число членов динамического ряда (показателей убыточности страховой суммы).

Сумма средних квадратических отклонений (числитель дроби под знаком квадратного корня) определяется с помощью данных табл. 2.

Таблица 2

Подставив данные таблицы в формулу (9), получим

                       (10)

Коэффициент вариации (V) при исчисленном значении σ

                            (11)

Подставив значения σ и  в формулу (11), получим

% = 4,7%                    (12)

В рассматриваемом примере линейные отклонения сначала возводятся в квадрат, чтобы избавиться от отрицательных значений некоторых линейных отклонений, а затем извлекается квадратный корень.

Размер тарифной нетто-ставки в рассмотренном примере будет составлять

      -15,8+0,75=16 руб. 55 коп                           (13)

где То — тариф нетто-ставки без рисковой (гарантийной) надбавки;

- средняя величина убыточности страховой суммы;

σ — среднеквадратическое отклонение суммы квадратических линейных отклонений к средней арифметической показателей убыточности страховой суммы (расчет рисковой надбавки изложен в Методике расчета тарифных ставок но рисковым вилам страхования).

Методика расчета нагрузки

Нагрузка — часть страхового тарифа, предназначенная для покрытия затрат на проведение страхования и создания фонда предупредительных мероприятий (ПМ). В ее составе может быть предусмотрена прибыль от проведения страховых операций.

Методика расчета нагрузки к нетто-ставке основана на определении фактических затрат по содержанию страховой организации или фактических накладных расходов страховщика. Они рассчитываются поданным действующей бухгалтерской и статистической отчетности за конкретное время, затем определяется их удельный вес (процентный) в сумме поступивших за тот же период страховых платежей.

Нагрузка (Н) определяется из равенства

Н = брутто-ставка — нетто-ставка.                       (14)

Размер совокупной тарифной, или брутто-станки, рассчитывается по формуле

Тбс = Тнс+Н,                                                      (15)

где Тнс - совокупный тариф нетто-ставки.

В равенстве (15) величины Т6с. Тнс и Н исчисляются в абсолютных размерах, т. е. в денежных единицах (д. е.), со 100 денежных единиц страховой суммы.

Если расходы на ведение дел (включая оплату труда) выражены в абсолютном значении, а на предупредительные мероприятия и планируемую прибыль — в процентах, то брутто-ставка определяется по формуле

                              (16)

где значения Тнс  выражены в абсолютных единицах,

Н – статья нагрузки выраженная в абсолютных единицах,

Н'— доля статей нагрузки, закладываемых в тариф, в процентах к брутто-ставке.

Если нее элементы (составляющие) нагрузки выражены в процентах относительно брутто-ставки, то значение Н будет равно нулю. Тогда формула (16) примет вид:

(д.е.), или                   (17)

Если в рассмотренном ранее примере тариф нетто-ставки Тнс = 16 руб. 55 коп.≈ 17 руб., а нагрузка в брутто-ставке, предположим, составляет 20%, то . Тогда нагрузка в денежном выражении Н = Тбс - Тнс = =21 - 17 = 4 руб.